New Page 1

§ 6. Применение производной к исследованию функции

199. Работа с книгой.

1) Найти в § 27 учебника ответ на вопрос: какое отношение имеет касательная к возрастанию или убыванию функции. Объясните своими словами.

2) Составьте логический план изложения темы "Экстремумы функции".

3) Имеется ли сходство между двумя утверждениями:

а) Если на промежутке, то функция возрастает на этом промежутке.

б) Если для функции на некотором промежутке из следует , то функция возрастает на этом промежутке.

4) Верно ли утверждение: если функция непрерывна на промежутке, то она имеет производную на этом промежутке. Ответ подтвердите цитатой из учебника.

5) Имеется ли связь между возрастанием (убыванием) функции и знаком производной этой функции?

6) Установите различие и сходство в определении точек максимума и минимума. Как вы объясните, что в записи неравенств существует знак равенства?

7) В чем заключается геометрический смысл теоремы Ферма? Ответ подтвердите соответствующим рисунком.

8) В чем заключается достаточное условие экстремума?

9) При переходе через стационарную точку производная может изменить свой знак. Какие при этом возможны варианты и каковы последствия для функции? Ответ подтвердите соответствующими рисунками.

10) Составьте тезисы к разделу: "Применение производной к исследованию функции".

11) Составьте план объяснения темы: "Применение производной к построению графиков функций".

12) Составьте аннотацию к главе 6 учебника.

13) Процитируйте из учебника те основные положения, которые необходимы при построении графиков с помощью производной.

14) В чем разница нахождения наибольшего и наименьшего значений функции на отрезке от аналогичных действий на интервале?

200 (Р). Объясните значений выражений: "Функция возрастает в интервале (-2;1)", "убывает в промежутке ".

201 (Вб). Опишите поведение графика функции и нарисуйте схематически её график, если известно: "возрастает на до 4", "убывает на (2;5) до -2", "принимает значение -2 на промежутке

202 (Р). Составьте предложение, используя выражения: возрастает, для любых, на множестве, если, функция f(x), чисел х1 и х2 , из множества М, f(x1)<f(x2), х1<х2, из неравенства, следует неравенство.

203 (П). Вставьте знаки >, < так, чтобы получилось правильное умозаключение:

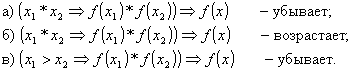
204 (Р). Устраните недостатки в речи учащегося, если его ответ был таким: "Возрастающая функция потому возрастает, что меньшему значению аргумента соответствует меньшее значение функции. Если бы было наоборот, то она убывала бы".

205 (Вн, П). Укажите промежутки возрастания и промежутки убывания функции, изображенной на графике (рис. 48):

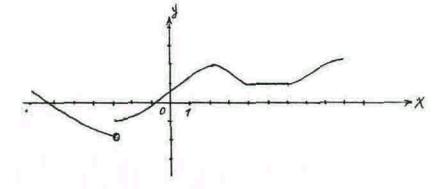
Рис.48

206 (Вн, П). Рассмотрите в течение 10 секунд рисунок 49, запомните его и воспроизведите на бумаге.

207 (Вп, П). На рис. 50 приводится график некоторой функции. В каком из промежутков: Докажите свои утверждения.

208 (Вп, П). На рис. 51 прочертите график той функции, для которой одновременно справедливы следующие утверждения:

209 (Р, П). Ответьте на вопросы:

1) Если функция возрастает в отрезке [a, b], то положительными или отрицательными числами будут угловые коэффициенты касательных к графику функции в точках, принадлежащих отрезку?. 2) Ответьте на тот же вопрос относительно функции, убывающей в отрезке [a, b].

210 (Р, П). Выполните задание:

1) Какой знак имеет производная в точках возрастания функции;

в точках убывания функции? Каковы необходимые условия возрастания и убывания функции в отрезке [a, b]?

2) Сформулировать достаточные признаки возрастания и убывания функции в отрезке [a, b]. Привести примеры, иллюстрирующие эти признаки.

211. Практическая работа. Построив графики функций у=2х+1 и у=2-4х установите их возрастание или убывание. Найдите производные. Нет ли между производной и поведением функции (возрастание, убывание) 0какой-нибудь связи? Сформулируйте её как теорему и докажите (под руководством учителя).

212 (П). Выполнив задание: "Найдите промежутки возрастания функции , двое учащихся написали ответ: Кто из них прав?

213 (П). Правильно ли сформулировано определение: "Точки, в которых производная функции не равна 0, называют стационарными"?

214 (П). Найдите ошибку в определении: "Точкой минимума функции f называется точка х0, если найдется такая окрестность этой точки, что для всех х0 из этой окрестности ".

215 (П). Какое из нижеследующих условий является достаточным, какое необходимым условием экстремума?

1) Если функция имеет экстремум, то .

2. Если в точке x0 производная меняет знак (с "+" на "-" или наоборот), то х0 есть точка экстремума.

216. Если данная функция имеет несколько экстремумов (больше двух), может ли случиться, что какой-нибудь максимум окажется меньше 0минимума?

217. Для функции с помощью графика её производной (рис. 52) найдите:

а) промежутки возрастания;

б) промежутки убывания;

в) точки максимума и минимума.

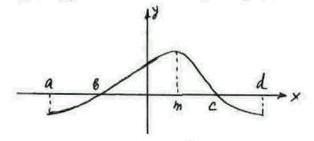
Рис.52

218. Обозначим буквой А утверждение "функция f имеет предел в точке x0", буквой B - утверждение "функция f непрерывна в точке x0", буквой C - утверждение "функция f имеет производную в точке x0". Определите, какие из следующих высказываний верны:

а) С Þ В; б) С Þ А; в) А Þ В;

г) если не В, то не С; д) если не С, то не В.

219. Составьте алгоритм нахождения наибольшего и наименьшего значений функций на отрезке.

220. Восстановите текст:

"Определите промежутки возрастания и убывания функции

П л а н р е ш е н и я. 1) Функция определена на множестве R.

3) , если ...>0 Û х<0. Функция у ... на промежутке

4) , если ...<0; -16х<... Û х>0. Функция у ... на промежутке

5) Так как функция непрерывна в точке х0=0, то у ... на промежутке и ... на промежутке

О т в е т. Функция возрастает на промежутке ...; функция убывает на промежутке ..."

221. Устраните ошибки в тексте:

"Определите промежутки возрастания и убывания функции

П л а н р е ш е н и я. 1) Функция определена на множестве R.

3) , если 2х-4<0: 2х-4<0 Û 2х<4 Û х<2. Функция возрастает на промежутке

4) , если 2х-4>0: 2х-4>0 Û х>2. Функция убывает на промежутке

5) Так как функция непрерывна в точке х0=1, то у убывает на промежутке и возрастает на промежутке

О т в е т. Функция возрастает на промежутке ; функция убывает на промежутке

222. Изучите блок-схему исследования функции на возрастание и убывание и используйте на практике (по А.А. Столяру).

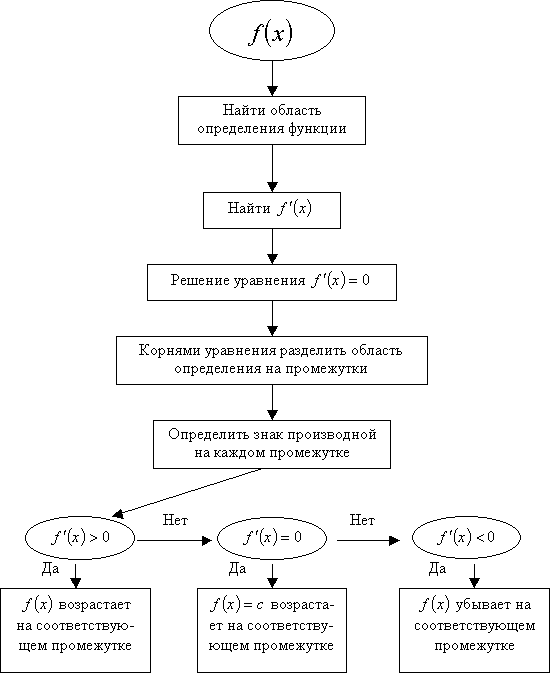
223. Изучите нижеследующее доказательство признака максимума функции и по аналогии докажите признак минимума функции.

П р и з н а к м а к с и м у м а ф у н к ц и и . Если функция f непрерывна в точке х0, а на интервале (a;x0) и на интервале (x0;b),то точка x0 является точкой максимума функции f.

Д о к а з а т е л ь с т в о. Производная на интервале (a;x0), а функция f непрерывна в точке x0, следовательно функция f возрастает на промежутке (a;x0], и потому f(x)<f(x0) для всех x из интервала (a;x0).

На промежутке [x0;b) функция f убывает (доказательство аналогично), и потому f(x)<f(x0) для всех x из интервала (x0;b).

Итак, f(x)<f(x0) для всех x¹x0 0из интервала (a;b), т.е. x0 есть точка максимума функции f.

П р и з н а к м и н и м у м а ф у н к ц и и. Если функция f непрерывна в точке x0, на интервале (a;x0) и на интервале (x0;b), то точка x0 является точкой минимума функции f.

224. Производная может быть применена к выяснению истинности неравенств. Изучите решение нижеследующего примера и самостоятельно решите второй пример.

1. Пусть Проверьте истинность неравенства

Р е ш е н и е. Рассмотрим на функцию . Найдем её производную: . Видим, что при Следовательно, f(x) 0на убывает, так что при Но Следовательно, данное неравенство верное.

2) Проверьте справедливость следующего утверждения: если х>2, то

225. Вставьте в тексте недостающие элементы:

"Сумма двух положительных чисел равна p. Каковы должны быть эти числа, чтобы их произведение было наибольшим?

Р е ш е н и е. Обозначим одно из слагаемых через х, тогда другое слагаемое будет ... Обозначим произведение этих чисел через у, тогда ...=у, где 0<х<p. После преобразований получаем у=...

Исследуем эту функцию с помощью производной:

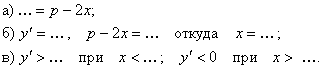
Следовательно, при х=... функция имеет максимум. Таким образом, произведение будет наибольшим при ... слагаемых.