§2. Логарифмическая функция.

31. Работа с учебником:

1.       Найдите в учебнике определение: а) логарифма; б) логарифмической функции и поясните их смысл на конкретных примерах.

2.       Выпишите из учебника формулы, выражающие различные свойства логарифмов. Сформулируйте их своими словами и приведите доказательство.

3.       Изучив материал о десятичных логарифмах определите, в чем заключается основная причина их возникновения.

4.       Составьте план и тезисы выступления по теме "Логарифмическая функция и её график".

5.       Из скольких частей состоит доказательство свойств возрастания и убывания логарифмической функции?

6.       Доказательство возрастания логарифмической функции в учебнике начинается так: "Пусть . Докажем, что если , то , т.е. ...". Проведите аналогичное доказательство, допустив: "Пусть . Докажем, что если , то ...".

7.       В чем причина того, что областью определения логарифмической функции является множество положительных чисел?

8.       После изучения главы 11 "Логарифмическая функция" из упражнений для итогового повторения курса алгебры выпишите номера упражнений, относящиеся к данной теме.

32 (Вн).Вставьте пропущенные элементы в определениях:

1.      Логарифмом числа b по основанию  называется показатель степени, в которую надо возвести число ....., чтобы получить число .....

2.      Функция, задаваемая формулой вида у =....... называется логарифмической.

33 (П). При каких а и b выражение  имеет смысл?

34 (П). Какое из нижеследующих операций называется логарифмированием?

1.      Операция нахождения числа по данному его логарифму.

2.      Операция нахождения логарифма числа или нахождения логарифма некоторого выражения.

35. Устраните ошибку при упрощении:

36 (Вн). На рис. 29 выделите графики логарифмической функции и определите их основание а: для каких а>1 или 0<а<1.

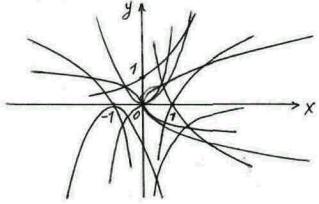
Рис.29

37 (Вн, Вп, П). В течение 10 секунд рассмотри рис. 30, запомни их и нарисуй на бумаге. После проверь!

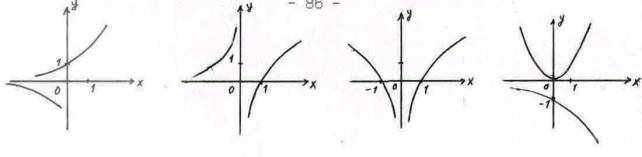
Рис.30

Сколько на рисунке графиков логарифмической функции?

38 (Вн). Установи стрелками соответствие (рис. 31) между свойствами логарифмической и показательной функций и соответствующими множествами (обозначения: D - область определения; E – множество значений;  - множество всех положительных чисел).

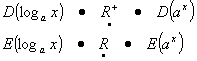
Рис.31

Какой вывод можно сделать по данному рисунку?

39 (Вн). Нарисуйте на бумаге графики логарифмической функции с любым основанием и проверьте правильность предложения "График функции проходит через точку (1;0)". Ответ проверьте по учебнику.

40. На рисунке 32 изображен график функции:

1.      Определить значения функции у при следующих значениях

2.      Истолковать при помощи графика, что: а) всякое положительное число имеет логарифм и притом только один; б) отрицательные числа и нуль не имеют логарифмов; в) логарифм 1 равен 0; г) логарифмы чисел, больших единицы, положительны, а логарифмы чисел, меньших единицы, отрицательны; д) при неограниченном возрастании числа от 0 до  логарифм его неограниченно возрастает от  до .

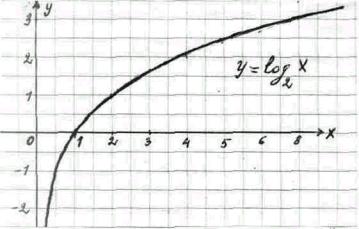
Рис.32

41. 1) Вычертить на одном и том же чертеже графики функций  давая х следующие значения:

Определить: а) свойства, общие для обеих функций; б) различие свойств функций  и .

2)                   Какое значение аргумента х является допустимым для функций:

3)     Какое заключение можно сделать относительно логарифмируемых чисел m и n, если:

4)                   Какое заключение можно сделать относительно логарифмируемого числа m, если:

5)                   Какое заключение можно сделать относительно основания логарифмов а, если:

42 (Вн, П). Найдите и устраните ошибки в следующих предложениях:

1.      Область определения логарифмической функции - множество всех действительных чисел:

2.      Область значений логарифмической функции - множество всех положительных чисел:

3.      На промежутке  логарифмическая функция при 0<а<1 возрастает, при а>1 - убывает.

43 (Вб). Задание выполняется в паре. Один из вас, закрыв глаза, руками в воздухе рисует график логарифмической функции и рассказывает её свойства. Другой контролирует и исправляет ваши ошибки. После поменяйтесь ролями.

44 (Вп). Выполните задания:

45 (Вп). Используя свойство логарифмической функции решите неравенство: а)  при х>0, б)  при х<0.

46 (Вп, П). Вместо звездочек вставьте соответствующие математические знаки и обоснуйте их:

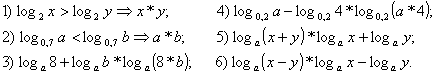
47 (П). Вместо точек вставьте рассуждения, которые обосновывают решение неравенства:

а)

б)

48 (П). Вернитесь к заданию 15 и проверьте свои записи: правильно ли вы "отгадали" свойства логарифмической функции? Какую роль при этом играет прямая у=х? Для ответа используйте и задание 38.

49 (П). Решите уравнение:

Покажите ответ на числовой прямой.

50. Прочитайте один раз нижеследующие слова, и, закрыв текст, запишите на бумаге. Результат проверьте.

Функция, уравнение, логарифм, следствие, множество, равносильны, обратные, корень.

51(П). Рассмотрите в течение 10 секунд рис.33, запомните, нарисуйте на бумаге и проверьте. Придумайте сами такое задание и предложите товарищу.

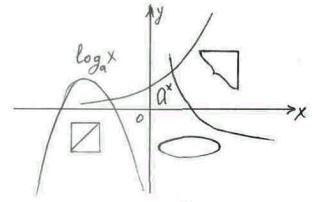
52(П, Р). Объясните смысл терминов "взаимно обратные функции", "следствие уравнения", "равносильные уравнения".

53 (Р). Из следующих слов: равносильными, не, два, корней, являются, имеющие, уравнения составьте связное высказывание.

54 (Р). Устраните ошибки в объяснении ученика: "Чтобы решить уравнение  умножим логарифмы и получим  Из этого по определению степени может написать  Раскроем скобки и получим  Отсюда  Проверим: а)  значит  подходит; б)  не имеет смысла, т.к. логарифм отрицательным быть не может. Ответ: х =1.

55 (Р). Устраните непоследовательность в тексте: "Решим уравнение  Это уравнение определено для тех значений х, при которых выполнены неравенства 2х+3>0 и х+1>0. Число х= -2 не удовлетворяет, однако неравенству х +1>0. Для этих х данное уравнение равносильно уравнению 2х+3=х+1, из которого находим х=-2. Следовательно, данное уравнение корней не имеет".

56 (Р). Оформите решение уравнения

а) в виде связного текста;

б) с применением символики.

57 (Р). Сопоставьте тексты § 8 главы 2 и § 2 главы 1 учебника, укажите общее в данных текстах и их отличия.

58 (Г). Напишите примеры, при решении которых используется возрастание или убывание логарифмической функции.

59 (Г). Напишите примеры, при решении которых используется определение логарифма.

60 (Г). Напишите уравнения, которые решаются аналогично уравнению

Какие математические правила или определения используются при их решении?

61 (Г). Не решая неравенства  ответьте: меняются ли рассуждения при переходе от решения одного из них к решению другого?

62. Найдите ошибки в решениях следующих уравнений и неравенств.

1) Решить неравенство:

Решение.

Ответ:

2) Решить неравенство:

Решение.

Ответ:

3) Решить уравнение:

Решение.

Ответ:

63. Где ошибка?

Произвольное число, отличное от нуля, равно нулю.

(по В.М. Брадису).

Пусть b - произвольное число, отличное от нуля.

Если а=-b,                                                                                                                     (1)

то очевидно,                                                                                                  (2)

Прологарифмировав соотношение (2) будем иметь

                                                                                                                 (3)

Введя новые обозначения:

                                                                                                         (4)

можно записать

На основании соотношения (3) и (4) утверждаем, что х=у, а потому

                         т.е. а = b                                                                               (5)

Складывая почленно равенства (1) и (5), имеем: 2а=0, т.е. а=0.

      Отсюда делаем вывод, что произвольное число, отличное от нуля, равно нулю.