и изложите его
своими словами.§ 1. Показательная функция
1.
Работа с учебником:
1)
Найдите в учебнике определение
показательной функции и процитируйте его.
2)
Найдите и прочитайте доказательство
возрастания показательной функции при
и изложите его
своими словами.
3)
Из упражнения для итогового повторения
курса алгебры выпишите номера упражнений,
которые относятся к показательной функции.
4)
Выделите основную мысль или идею в случае,
когда в тексте учебника приводится формула
радиактивного распада.
5)
Выделите узловые вопросы и основные факты,
необходимые для запоминания содержания
темы «Свойства показательной функции и ее
график».
6)
Еще раз прочитайте определение
показательной функции и выясните, чем она
отличается от степенной функции.
7)
Приведите примеры из жизни, где применяется
понятие показательной функции.
8)
Чем объяснить, что уравнение
имеет единственный
корень
?
9)
Какие теоретические положения
используются при решении неравенств вида
или
?
10)
Равносильны ли рассуждения:
а)
Функции
как видно из их
графиков (см. учебник), возрастают. Значит,
функция
при
возрастает.
б)
Функция
при
возрастает. Значит
функции
- возрастающие.
2.
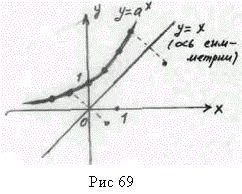
(Вн). На
рис.23 покажите графики показательной
функции и определите, какие из них имеют
основанием: а) целое число; б) дробное число;
в) отрицательное число; г) число 1.
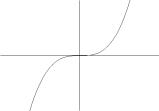
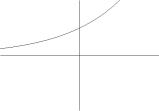
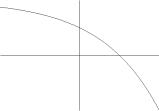
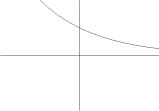
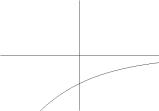
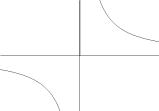
Рис.23
3 (Вн). На рис. 24 приведены графики известных вам функций. Определите графики и назовите эти функции.
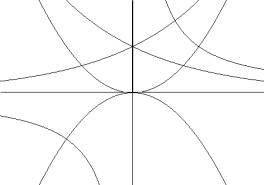
Рис.24
4
(Вп).
Нарисуйте на бумаге график показательной
функции с любым основанием и проверьте
правильность предложения: «График функции
проходит через
точку
». Ответ проверьте по учебнику.
5
(Вп).
Проведите стрелки от показательных функций
к их основаниям:
Функция
Основание
6
(Вп).
Правильно ли сформулированы свойства
показательной функции:
1)
Область определения показательной функции
- множество всех положительных чисел.
2)
Множество значений показательной функции -
множество R
всех действительных чисел.
3)
Показательная функция
является
возрастающей на множестве действительных
чисел, если
; если же
- то убывающей.
7
(Вп, Лм).
На рис. 25 изображен график функции
. Используя график, закончите
предложения:
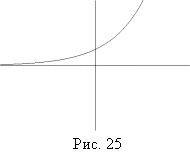
1)
При любом значении
функция
2)
при
значение
3)
при
значение
4)
при изменении
от
до
функция
5)
при
значение
8.
Какое заключение можно сделать
относительно чисел
и
(сравните их), если
даны разные значения показательной функции:
1)
2)
3)
4)
9.
График функции
проходит через
точку М(1;3).
1)
Найдите основание а.
2)
Определите, что больше:
или
3)
Сравните числа
и 1.
При
ответах на 2) и 3) используйте свойства
функции
.
10.
Вместо * вставьте соответствующий знак и
сформулируйте правило:
1)
2)
Запомните:
на этих теоремах основано решение
показательных уравнений.
11
(Вб).
Мысленно «нарисуйте» графики функций
и
. Что общего вы «видите» на чертеже?
Результат проверьте письменно.
12
(Вб).
Задание выполняется в паре. Один из вас
закрыв глаза руками в воздухе "рисует"
график функции
(возрастающей или
убывающей) и рассказывает её свойства.
Другой контролирует. Ошибки уточните по
тексту учебника.
13.
В формулах вставьте недостающие члены и
сформулируйте соответствующие правила,
известные вам из предыдущего курса алгебры.
а)
г)
б)
д)
в)
14
(Вб, Об).
Закончи текст: «Формулу
можно прочитать
так: при возведении
дроби
в степень можно возвести в эту степень
числитель и знаменатель, и результаты
соответственно разделить.
Эту
же формулу можно прочитать обратно: при
делении степеней...
15
(Вб, Об).
Закончите рисунок (рис.26) и соедините
полученные точки. Не забудьте это задание.
Полученная линия является графиком
изучаемой в дальнейшем функции.
Попытайтесь написать его свойства (как в
задании 6) и сохраните для проверки в
дальнейшем.
16
(П).
Составьте мысленно план вашего выступления
на уроке по теме «Свойства показательной
функции и её график».
17
(П). В
решении уравнения вместо точек вставьте
правила (устно), которые являются
основанием для последующей записи:
откуда
.
18
(П). В
математике полезно ориентироваться не
просто образцу решения, а, прежде всего, -
образцу рассуждения. Ниже приводится
вариант беседы при решении уравнений, где
при рассуждениях используется прием
соотнесения, т.е. изучаемое новое положение
связывается с ранее известным. Изучи его и
реши аналогичными рассуждениями
предлагаемые уравнения.
1.
Решить уравнения: а)
, б)
.
Решение,
а) Объясняя решение уравнения
, в учебнике пишут: "запишем уравнение в
виде
. А почему именно так? Как догадаться, что
надо сводить к теореме? А если не догадаюсь?
Вот как это делается.
-
Какая у нас показательная функция и с каким
основанием? (
, основание 2). Было бы нам удобно, если бы
везде были написаны ... (Двойки!) Напишем: 4 -
это...
, а 1 -это...
. Что получим?
Было бы удобно,
если бы этих двоек было ... (Поменьше!)
Сделаем. (Слева
, по свойству произведения степеней, равно
, тогда
). По свойству равенства степеней получим:
и
. Записываем ответ:
.
б)
Решение уравнения
в учебнике
начинается так: "Заменой
данное уравнение
сводится к квадратному..." А почему замена?
Почему квадратное? А как самому догадаться?
Приводим рассуждения, которые должен
усвоить ученик в данном случае.
Мне
удобно, если было бы не две функции
и
, а только одна:
. Но тогда вместо 9 должно быть 3. Пишу:
. Используя правило возведения степени
в степень, убираю скобки, запись будет проще:
. Основания я сделал одинаковой, но
показатели разные. Мне нужно, чтобы везде
было
. А если попробовать так:
, тогда уравнение примет такой вид:
, т.е. оно имеет такую форму:
Это же квадратное
уравнение! Значит вместо
надо писать какую-то
букву, т.е. заменить
. Получим уравнение
, находим его корни:
откуда
Уравнение
имеет корень
, а уравнение
не имеет корней,
так как показательная функция не может
принимать отрицательные значения. Ответ:
.
2.
Решите уравнения: а)
; б)
аналогичными
рассуждениями.
19
(П).
Решите уравнение
.
20
(П).
Решите уравнение
при условии, если
.
21
(П).
Прочитайте внимательно следующие слова
один раз, запомните и воспроизведите вслух.
После проверьте!
а)
Число, значение, действительное, множество,
функция, все, показательная, множество, есть.
б)
, четверть,
, вторая, график, первая, показательная,
расположен, функция, при, в.
22
(П). В
течение 10 сек. рассмотри рис. 9, запомни и
нарисуй на бумаге. Проверь, сколько ты
запомнил.
23
(Г).
Составьте показательные уравнения, которые
решаются:
а)
вынесением показательной функции как
общего множителя за скобки;
б)
сведением к квадратному уравнению.
24
(Г, Вб).
1) Решите неравенство
.
2)
Найдите рациональный способ решения
неравенств:
a)
б)
в)
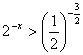
25.
Найдите ошибки в решениях нижеследующих
уравнений и неравенств (из работ учащихся):
1)
Решить уравнение:
.
Решение.
.
Обозначив
получим
.
По
формуле корней квадратного уравнения имеем
.
Ответ:
.
2)
Решить неравенство:
Решение:
.
Ответ:
.
3)
Решить неравенство:
.
Решение.
.
Так
как функция убывающая, поэтому знак
неравенства меняем на противоположный:
.
Ответ:
.
4)
Решить неравенство:
.
Решение.
.
Так
как функция
убывающая, поэтому
, т.е.
.
Ответ:
.
26
(Р)
Оформите решение уравнения
.
а)
в виде связного текста (см. № 17); б) с
применением символики.
27.
Продолжи ряд:
а)
б)
28
(Р)
Используя блок-схему на рис. 70, расскажите
общий метод решения простейших
показательных уравнений и приведите
конкретный пример:
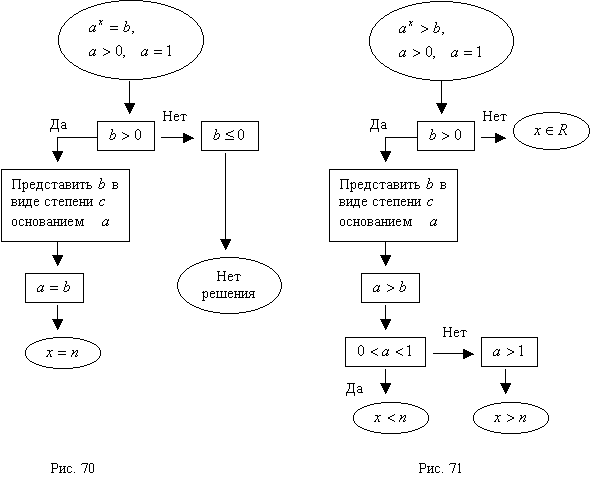
29
(Р).
Используя блок-схему на рис. 71, расскажите
общий метод решения простейших
показательных неравенств и приведите
конкретный пример.
30.
Вы согласны?
Положительная
единица равна отрицательной единице (по В.М.
Брадису).
Пусть
- есть
положительное число, отличное от единицы.
Определим
число
так, чтобы
(1)
Исходя
из этого соотношения, утверждаем, что
.
Легко
видеть, что
, так как по условию
.
Из
этого же вывода следует, что
.
(2)
Сопоставив соотношение (1) и
(2) устанавливаем, что
.
