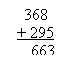
§ 3. Тысяча

В концентре "Тысяча" продолжается работа над устными и письменными приемами сложения и вычитания, которые вводятся и для трехзначных чисел. Рассматриваются устные приемы умножения и деления с разрядными числами.

В результате изучения действий над числами в пределах 1000 учащиеся наряду с устными, должны усвоить алгоритмы письменного сложения и вычитания.

Сложение и вычитание в пределах 1000.

При изучении сложения и вычитания в качестве подготовительной работы повторяют:

- нумерацию чисел, и в особенности, представление чисел в виде суммы разрядных слагаемых;

- соответствующие математические правила;

- аналогичные случаи сложения и вычитания с двузначными числами.

Методика введения всех приемов основана на аналогии с использованием приема соотнесения (см.гл.3, §5 ). Например, при рассмотрении приема вычисления вида 250+20, учитель предлагает пример 50+30 и просит объяснить его решение (5 дес.+3 дес.=8 дес., т.е. 50+30=80). Далее выясняет: почему мы 50 представили как 5 десятков? (Тогда сложение десятков сводится к сложению единиц.) Нельзя ли и здесь свести сложение к более низким разрядам? (Можно, 250 это 25 десятков, 20 - 2 десятка, 25 дес.+2 дес.=27 дес., т.е. 250+20=270.) В тетради записывают:

250+20=270

25 дес.+2 дес.=27дес.

нижняя запись в которой по мере сокращения рассуждений "исчезает".

Сложение и вычитание вида 600+300 учащиеся выполняют устно, а 840+60, 800-30 при первоначальном ознакомлении записывают:

840+60=(800+40)+60=800+100=900

800-30=(700+100)-30=700+70=770

и после переходят на устную форму работы. Здесь возможны записи решения 840+60=80 дес.+6 дес.=9 дес.=900, 800-30=80 дес.-3 дес.=77 дес.= 770, которые запрещать не следует.

При ознакомлении с письменным сложением и вычитанием учитель предлагает выполнить, например, сложение 68+95 столбиком с полным объяснением и спрашивает: что изменится, если впереди этих чисел напишем сотни, например, 368 и 295. Учащиеся отвечают, что правило сложения остается таким же, по появляется еще один разряд. Далее выполняют сложение по алгоритму:

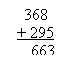
1) Пишу

2) Складываю единицы: 8+5=13; 13 - это 1 дес. и 3 ед.,

3 ед. пишу под единицами, 1 дес. запоминаю.

3) Складываю десятки: 6+9=15; еще 1 дес. будет 16 дес. Это 1 сот. 6 дес.; 6 дес. пишу под десятками, 1 сот. запоминаю.

4) Складываю сотни: 3+2=5, еще 1 сот. и будет 6 сотен.

Под сотнями пишу 6.

5) Читаю ответ..

Затруднения вызывает случаи вычитания вида 506-288. В этом случае первоначальное объяснение целесообразно провести так:

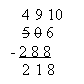
Из 6 единиц вычесть 8 единиц не можем, из десятков занимать не можем; из 5 сотен беру 1 сотню, там останется 4 сотни (5 зачеркиваю, записываю 4). 1 сотню переносим в разряд десятков, это будет 10 десятков. Из 10 десятков беру 1 десяток, там останется 9 десятков (записываю 9) и перенесем в разряд единиц. У нас будет 10 единиц и еще 6 единиц, будет 16 единиц. Из 16 единиц вычитаю 8 единиц, будет 8, из 9 десятков ... и т.д.

Постепенно написанные сверху числа 4 и 9 заменяются точками, которые по мере формирования навыков тоже "исчезают".

Умножение и деление в пределах 1000.

В концентре "Тысяча" рассматриваются следующие приемы устных вычислений:

которые сводятся к табличному умножению и делению разрядных чисел. Используя аналогию с умножением и делением в пределах 100, учитель может добиться самостоятельного объяснения учащимися этих приемов вычислений.