§ 2. Сотня

В результате изучения арифметических действий в концентре "Сотня" учащиеся должны:

- осознанно выполнять устные и письменные вычисления с объяснением их решения по соответствующим правилам;

- твердо усвоить табличные случаи сложения и вычитания с переходом через десяток;

- знать конкретный смысл новых действий: умножения и деления, связь между компонентами и результатом действий;

- знать таблицу умножения и деления;

- знать табличные и внетабличные случаи умножения и деления;

- знать формулировки изучаемых правил и уметь применять их в соответствующих случаях.

Сложение и вычитание в пределах 100

В 1 классе изучаются математические свойства и приемы вычислений:

1) сложение и вычитание с переходом через десяток;

2) сложение и вычитание разрядных чисел: 40+20, 50-30;

3) прибавление числа к сумме и на его основе: 34+20, 34+2, 26+4;

4) вычитание числа из суммы и на его основе: 48-30, 48-3, 30-6;

5) прибавление суммы к числу и на его основе: 47+5, 40+16, 45+12;

6) вычитание суммы из числа и на его основе: 42-5, 40-16, 45-12.

Во 2 классе изучаются письменное сложение и вычитание столбиком без перехода и с переходом через десяток.

Рассмотрим методику изучения этих вопросов:

1. Сложение с переходом через десяток (9+2, 8+6 и т.п.) и вычитание с переходом через десяток (12-4, 15-7 и т.п.) может быть изучено применением интегральной технологии обучения (см. гл. 5, § 9). При отдельном изучении каждого примера целесообразно применять технологию поэтапного формирования умственных действий.

Подготовительной работой к изучению этого случая сложения и вычитания является повторение состава чисел от 2 до 10. При изучении, например, сложения 8+5 учащиеся работают на наборном полотне: к 8 кружочкам в первом ряду добавляют 2 кружка и во второй ряд ставят оставшиеся 3 кружка. Потом делают вывод: чтобы к 8 прибавить 5, сначала прибавив 2, дополняем до 10 и после прибавим 3:

     8+5=8+2+3=13.

          /\ 

         2 3

Во всех примерах на сложение с переходом через десяток все время делаем главный вывод: сначала число, к которому прибавляем, дополняем до 10, используя состав второго числа и затем прибавим оставшуюся часть.

При изучении вычитании вида 13-5 работаем аналогично, употребляя термин "доводим до 10" (см. также гл. 4, § 9). Нужно обратить внимание учащихся на то, что число единиц 3 подсказывает, какое число сначала надо вычесть и при этом для запоминания эффективна такая модель (рис.93).Изучение сложения с переходом через десяток завершается составлением таблицы сложения.

2. Изучение сложения и вычитания разрядных чисел, например сводится к и вычитанию чисел в пределах 10 (4 дес.+3 дес.=7 дес., т.е. и т.д.).

3-4. Методика изучения темы "Прибавление числа к сумме: (4+3)+2 полностью аналогична методике изучения темы "Вычитание числа из суммы (4+3)-2", о которой мы уже говорили (гл. 2, § 1; гл. 3, § 7 и гл. 4, § 8). На основе этих правил учащиеся рассматривают следующие приемы вычислений:

34+20=(30+4)+20=50+4=54

34+2=(30+4)+2=30+6=36

26+4=(20+6)+4=20+10=30

48-30=(40+8)-30=10+8=18

48-3=(40+8)-3=40+5-45

30-6=(20+10)-6=20+4=24.

При подготовке к их изучению повторяют представление числа в виде суммы разрядных слагаемых и соответствующие правила (см. также гл. 2, § 7; гл. 7 - § 2; гл. 4, § 6).

При изучении этих приемов оправдывает себя следующая методика. Учитель пишет на доске пример (3+4)+2 и повторяют различные способы её решения. После этого к числам 3 и 2 приписывает нули и получив пример (30+4)+20, просит обсудить, что при этом изменилось, а что - нет.(Изменились числа в примере, а прием вычисления останется такой же.) Записав удобным способом решение, учитель просит продолжить запись "справа налево" так, чтобы из примера с тремя числами оставить пример с двумя числами. Совместно получают запись 34+20=(30+4)+20=50+4=54. После этого еще раз повторяют решение и делают соответствующий вывод.

Используемый при такой методике прием соотнесения улучшает понимание и осмысление приема вычисления и тем самым его запоминание.

5-6. Методика изучения тем "Прибавление суммы к числу: 4+(2+1)" и "Вычитание суммы из числа: 7-(2+1)" аналогична методике изучения вышеназванных тем (см. также гл.4, § 1; гл.5, § 2; гл.2, § 7).На их основе рассматриваются следующие приемы вычислений:

а) 47+5=47+(3+2)=50+2=52

                      /\

                    3 2

или другая запись: 47+5=47+323=52

                                                   /\

                                                 3 2   

б) 42-5=42-(2+3)=40-3=37

                     /\ 

                   2 3

или другая запись: 42-5=42-2-3=37.

                                                  /\ 

                                                2 3

После закрепления всех правил и приемов вычислений далее на разных уроках одновременно рассматриваются пары примеров вида:

а) 40+16=40+(10+6)=50+6=56

40-16=40-(10+6)=30-6=24

б) 45+12=45+(10+2)=55+2=57

45-12=45-(10+2)=35-2=33.

При изучении всех вычислительных приемов ведется такая же подготовительная работа как и для случая 34+20, широко используются аналогия, различные опорные схемы (рис.94).

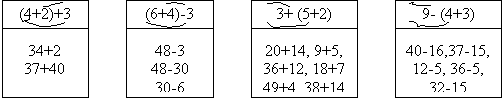
Рис.94

Во 2 классе рассматриваются письменные вычисления, которые записываются столбиком. Используя метод объяснения, учителю не составляет труда убедить учащихся в их целесообразности. Доступен для учащихся и метод самостоятельной работы с учебником: объясняют по рисунку решения примеров в строчку, а запись столбиком продолжает объяснять учитель.

Рассматриваются примеры на сложение и вычитание без перехода и с переходом через десяток:

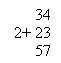
1) Пишу десятки под десятками, а единицы под единицами.

2) Складываю единицы: 4+3=7, пишу 7 под единицами.

3) Складываю десятки: 3+2=5, пишу под десятками 5.

4) Читаю ответ: сумма равна 57.

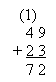
1)                 Пишу десятки под десятками, а единицы под единицами.

2)                 Складываю единицы: 9+3=12, 12 – это 1 дес. И 2 ед.; пишу под единицами 2, а 1 дес. запомню (указываю над десятками, можно запомнить просто и так) и прибавлю к десяткам.

3)                 Складываю десятки: 4+2=6, да еще 1 дес., получится 7. Пишу 7 под десятками.

4)                 Читаю ответ: сумма равна 72.

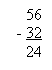
1)                 Пишу десятки под десятками, а единицы под единицами.

2)                 Вычитаю единицы из единиц: 6-2=4. Пишу 4 под единицами.

3)                 Вычитаю десятки из десятков: 5-3=2. Пишу 2 под десятками.

4)                 Читаю ответ: разность равна 24.

1) Пишу десятки под десятками, единицы под единицами.

2) Вычитаю единицы: из 2 нельзя вычесть 4; беру 1 дес. из 7 дес. (чтобы помнить об этом можно над 7 поставить точку или написать 6). 1 дес. и 2 ед. это 12, 12-4=8, под единицами пишем 8.

3) Вычитаю десятки. Стало не 7, а 6 дес. 6-3=3; пишу под десятками 3.

4) Читаю ответ: разность равна 38.

В учебниках отсутствуют формулировки вышеназванных правил и поэтому учителю полезно на стенде оформить справочные материалы в виде таблицы 25 и еще лучше иметь индивидуально у каждого ученика (включены примеры и из другого концентра).

Таблица 25

При изучении сложения и вычитания в пределах 100 учащиеся знакомятся с приемами проверки сложения и вычитания (используется метод самостоятельной работы):

Изучение проверки вычитания вводится после изучения правил нахождения неизвестного уменьшаемого и вычитаемого (методику их изучения см. в гл. 2, § 4; гл. 4, § 1).

Сложение и вычитание закрепляются в ходе решения примеров на вычисление, составление выражений и нахождение их значений, решения целесообразных задач.

Умножение и деление в пределах 100

В результате изучения умножения и деления учащихся должны:

- понимать конкретный смысл умножения и деления, уметь решать задачи, связанные с этими действиями;

- знать переместительное свойство умножения, связи между компонентами и результатом действия;

- твердо знать таблицу умножения и соответствующие случаи табличного деления;

- знать правила порядка выполнения арифметических действий, куда входят умножение и деление;

- овладеть приемами умножения и деления двузначных чисел на однозначное, деления двузначного числа на двузначное на основе правил умножения и деления суммы на число;

- знать особые случаи умножения и деления, связанные с числами 0 и 1.

Изучение умножения и деления подразделяют на несколько случаев:

1) табличное умножение (умножение чисел 2,3,...9) и соответствующие случаи деления;

2) внетабличное умножение и деление: умножение и деление двузначного числа на однозначное, умножение однозначного числа на двузначное и деление двузначного числа на двузначное (например, 12·3, 3·12, 48:3, 48:16);

3) умножение и деление, связанное с числами 0 и 1;

4) деление с остатком.

Рассмотрим методику работы над каждым из этих случаев.

Табличное умножение и деление начинается с раскрытия конкретного смысла умножения. После этого изучаются умножение числа 2, перестановка множителей (и на этой основе - умножение на 2). Далее рассматривается конкретный смысл деления, нахождение неизвестного множителя, делимого, делителя. Вводятся приемы умножения и деления с числами 1, 10 (1∙5, 5:1, 10∙4, 4∙10, 40:4, 40:10). После изучения этих вопросов изучаются табличное умножение 2, 3, ... 9 и соответствующие случаи деления; умножение и деление с числом 0. Изучив умножение суммы на число, рассматривают примеры вида 20∙4, 60:2, 3∙20, 60:20, 23∙4, 5∙14. Вводится правило деления суммы на число и на этой основе изучают приемы вычислений вида 46:2, 48:3. Изучение умножения и деления завершается делением вида 68:17, делением с остатком и ознакомлением проверкой деления и умножения.

Ознакомление с умножением учитель может провести так (см. также гл.2, § 6):

Предлагают учащимся обвести в тетради 3 раза по 2 клеточки:

- Сколько всего клеточек вы обвели? (6.) Как узнали? (2+2+2=6.) Запишем эту сумму. Какие слагаемые в этой сумме? (Одинаковые.) Сколько их? (3.) Примеры на сложение одинаковых чисел можно заменять примерами на умножение. (Записывает на доске, а дети в тетрадях: 2·3=6.) Точка - знак умножения. Число 2 показывает, какое слагаемое брали; число 3 показывает, сколько одинаковых слагаемых. Читается этот пример так: по 2 взять 3 раза, получится 6, или так: 2 умножить на 3, получится 6.

Дети еще раз читают запись и после этого для закрепления проводят аналогичную работу по рисунку и записям в учебнике.

Для закрепления умножения на следующих уроках предлагают упражнения вида:

1) Замени пример 6+6+6 примером на умножение.

2) Замени пример 5∙3 примером на сложение.

3) Можно ли пример 5+5+5+4 заменить примером только на умножение? Почему?

При выполнении таких примеров еще раз выясняем, что означают числа 6 и 4 в записи 6∙4 (6 - берется слагаемым, 4 - столько берется одинаковых слагаемых 6).

Изучение таблицы умножения числа 2 для учащихся не представляет труда: каждый пример сводится к нахождению суммы одинаковых слагаемых: 2∙5=10, т.к. 2+2+2+2+2=10. Для эффективного запоминания полезно его составлять не последовательно, а "вразброс" (см. составление таблицы сложения). После составления таблицы целесообразно сделать вывод: первый множитель не изменяется, второй - увеличивается на 1, а произведение каждый раз увеличивается на 2 (запоминание не требуется!).

Изучение переместительного свойства умножения (см. гл. 2, § 4 и гл. 4 § 4) завершается формулировкой правила: от перестановки множителей произведение не изменяется. После этого составляют таблицу умножения на 2, где пример 4∙2 решается на основе примера 2∙4.

Понятие деления вводится через задачу. С учащимися проводится такая работа.

- Возьмите 10 квадратов, разложите их по 2 квадрата. Сколько раз по 2 квадрата получилось? (5 раз.) Для решения этой задачи 10 разделили на 2, получили 5, вы выполнили действие деления.

Записывают решение задачи так:

10:2=5

Ответ: 5 раз.

Две точки - знак деления. Запись читают так: "10 разделить на 2, получится 5".

Для закрепления знания о делении рассматривают рисунок учебника, объясняют записи.

Два вида деления: по содержанию на равные части так же вводятся через задачи (см. гл. 7, § 7).

Правило нахождения неизвестного множителя можно изучить: а) используя рисунки учебника, б) работая с наглядными пособиями, в) используя моделирование. Рассмотрим последний вариант.

После изучения этого правила и ознакомления с названиями чисел при делении: делимое, делитель и частное, завершается работа с таблицей умножения 2, куда добавляются и соответствующие случаи деления, например, 2∙4=8, 4∙2=8, 8:2=4, 8:4=2 и т.д. Аналогично составляются таблица умножения 3,4...9 с соответствующими случаями деления. Заметим, если результат первого примера в этой строке, например, 3∙5 находится подсчетом числа квадратов по рисунку, то остальные 5∙3=15, 15:5=3, 15:3=5 решаются только рассуждениями на основе вышеназванных правил.

По мере составления таблиц умножения, число примеров уменьшается, например, для числа 9 остается: 9 9=81, 81:9. "Исчезновение" других примеров объясняется по аналогии с таблицей сложения.

При изучении правила нахождения неизвестного делимого и делителя (методику см. в гл. 2, § 4) учителю нужно добиться запоминания правил с полной формулировкой. На них основано деление с приемом подбора частного. При изучении внетабличного деления вида 51:17 пользуются этим приемом.

Ознакомление с приемом подбора частного учитель проводит так.

- Решим пример 12:4= не по таблице, а рассуждениями по правилам. Что неизвестно в этом примере? (Частное.) Знаем ли мы делитель? (Да, 4.) Какое правило мы знаем, где сказано о частном и делителе? (Если частное умножить на делитель, то получится делимое.) Найдем, на какое число надо умножить делитель 4, чтобы получить делимое 12: 4·2=8, число 2 не подходит; 4·3=12: значит 12:4=3. Этот прием будем называть подбором частного и он нам понадобится при делении двузначных чисел.

Умножение вида 1·5 разъясняется через сложение: 1+1+1+1+1=5, поэтому 1·5=5. После выполнения аналогичных упражнений, делаем вывод: при умножении единицы на любое число, получается то число, на которое умножали. Умножение вида 5·1=5 учащимся сообщается в готовом виде: при умножении любого числа на единицу, получается то число, которое умножали. Здесь невозможно использовать прием замены произведения суммой (т.к. в выражении 5·1=5 нет суммы) и поэтому нельзя опираться и на перестановку множителей (при перестановке множителей 2·3 и 3·2 оба примера возможно заменить сложением).

При делении 3:1 пользуемся подбором частного: найдем число, которое при умножении на 1 дает 3; это число3; поэтому 3:1=3.

В случаях умножения и деления вида 10·4, 4·10, 40:4, 40:10 рассуждают так:

а) чтобы умножить 10 на 4, надо 1 десяток умножить на 4, получится 4 десятка, или 40, т.е. 10·4=40;

б) 10·4=40, переставим множители и получим 4·10=40;

в) 10·4=40, тогда произведение делим на один из множителей и получим: 40:4=10, 40:10=4.

Случаи умножения и деления с нулем объясняются так:

а) 5·0=0 - сообщается в готовом виде: при умножении любого числа на нуль получается нуль;

б) 0:2=0, т.к. 0·2=0, поэтому при делении нуля на любое другое число получается нуль;

в) 6:0 - нельзя, есть правило: делить на нуль нельзя.

Внетабличное умножение и деление начинается с изучения правила умножения суммы на число. Рассмотрим методику ознакомления с этим правилом (прием М.И. Моро и других).

В качестве подготовки к новому полезно поупражнять детей в записи под диктовку выражений вида: "сумму чисел 10 и 8 разделить на 2"; "сумму чисел 6 и 3 умножить на 2" и т.п.

Ознакомить с различными способами умножения суммы двух слагаемых на какое-либо число можно так: под диктовку учителя дети записывают в тетрадях выражение "сумму чисел 3 и 4 умножить на 2". Далее в одном из рядов наборного полотна выкладываются, например, 3 красных и 4 синих кружка. Учитель спрашивает: "Что значит умножить на 2? Как это понять?". Выясняется, что умножить на 2 - это значит повторить сумму чисел 3 и 4 слагаемым два раза. Учитель выставляет во втором ряду наборного полотна еще раз 3 красных и 4 синих кружка и, показывая на все эти кружки, предлагает детям рассказать, как можно узнать, сколько всего кружков. Прежде всего нужно рассмотреть решение, вытекающее из записи: в каждом ряду всего 3+4=7 кружков, а рядов два. В двух рядах всего 7·2=14 кружков. Затем учитель предлагает внимательно посмотреть на полотно и подумать, как еще по-другому можно подсчитать, сколько всего кружков выставлено. Рассматривается такое решение: сначала узнаем, сколько всего красных кружков (3·2=6), а потом сколько всего синих (4·2=8), всего кружков будет: 6+8=14. Параллельно с разбором каждого

из этих способов решения учитель выполняет на доске соответствующие записи:

(3+4)·2=7·2=14

(3+4)·2=3·2+4·2=6+8=14

Сравнив полученные результаты, легко убедиться, что и тот и другой способ дают одинаковый ответ на поставленный вопрос. Кто-либо из вызванных учеников объясняет, как выполнялись вычисления в первом случае и как во втором.

После этого ученики самостоятельно рассматривают два способа решения предложенной в учебнике задачи и по вызову учителя устно объясняют каждый из них.

Изучение темы завершается формулировкой правила: чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные результаты сложить.

Для закрепления используются упражнения вида:

1) вычисли значение выражения двумя способами: (6+4)·10;

2) объясните, каким из способов можно найти значение выражения (8+9)·7;

2)       вставьте недостающие числа: (6+ □)·7=□·□ +4· 7=

□ + □ = □.

Целесообразно распространить правило и на случай трех слагаемых решением примеров (3+2+4)·3 двумя способами и соответствующим выводом. Это понадобится при изучении умножения трехзначных чисел на однозначное.

После изучения этого правила вводится умножение двузначного числа на однозначное вида 23·4=(20+3) ·4=20·4+3·4=80+12=92 (см.гл.4, § 3;§7, гл.5, § 1; гл.3, § 5). Умножение вида 5·14 рассматривается на основе переместительного свойства умножения: 5·14=14·5=70.

Деление двузначного числа на однозначное начинается с изучения темы "Деление суммы на число", которое может быть проведено следующим образом (прием М.И. Моро, М.А. Бантовой).

Различные способы деления суммы на число лучше всего продемонстрировать детям на наглядных пособиях. Так, учитель сообщает детям задачу: "6 красных яблок и 8 зеленых разложили поровну на 2 тарелки. Сколько яблок положили на каждую тарелку?"

Показывая детям соответствующие предметные картинки (6 красных и 8 зеленых яблок), учитель кладет их в пакет и предлагает кому-либо из детей разделить эти яблоки поровну, разложив их на 2 блюдца (на 2 полочки наборного полотна). Вызванный ученик должен каждый раз, доставая по 2 карточки, выставлять их затем по одной на каждую полочку. При этом, конечно, может оказаться и так, что оба вытянутых им яблока будут красными (или зелеными). Тогда на каждой полочке прибавится по одному одинаковому яблоку, но может оказаться и так, что в паре окажутся разные яблоки. Тогда на одной полочке добавится красное яблоко, а на другой - зеленое. Учитель подчеркнет, что обращать внимание на это не следует, так как в задаче требуется только, чтобы на блюдцах было поровну яблок, но не сказано, каких именно. В результате практического решения задачи выясняется, что на каждом блюдце стало по 7 яблок. Решение задачи повторяется кем-либо из вызванных учеников и на доске делается запись, соответствующая рассмотренному способу решения: (6+8):2=7 (ябл.)

Затем учитель предлагает детям разложить те же яблоки так, чтобы на обеих тарелках было поровну зеленых и красных яблок. Проводится соответствующая демонстрация: сначала делятся поровну на 2 равные части 6 красных яблок (на каждой полочке оказывается их по 3), затем - 8 зеленых (на каждой полочке по 4), а потом выясняется, сколько всего яблок на каждой полочке. По ходу повторения решения на доске выполняется запись: 6:2+8:2=3+4=7 (ябл.). Сравнив ответы, полученные в обоих случаях, дети убеждаются, что оба эти способа решения дали одинаковые результаты. После этого под руководством учителя дети сравнивают, чем отличались способы решения: в первом случае сначала узнали сумму двух чисел и разделили ее на 2, а во втором случае разделили на 2 каждое слагаемое в отдельности, а затем сложили полученные результаты.

Аналогично рассматриваются два способа решения задачи, которая дана для объяснения в учебнике.

Изучение темы завершается формулировкой правила: чтобы разделить сумму на число, можно на это число разделить каждое слагаемое и результаты сложить.

Для закрепления используются упражнения вида:

1) вычисли значение выражения двумя способами: (10+4):2;

2) объясни, каким из способов можно найти значения выражений: (11+13):6, (70+14):7;

3) вставьте недостающие числа:(30+□):3=□ :3+21:3=

□ + □ = □;

4) реши удобным способом: (50+10):5, (36+24):2.

Полезно решить несколько примеров вида (8+6+2):2 двумя способами, сделав соответствующий вывод. Это облегчит в будущем объяснение деления трехзначного числа на однозначное.

Перед ознакомлением решением примеров вида:

46:2=(40+6):2=40:2+6:2=20+3=23, необходимо повторить представление числа в виде суммы разрядных слагаемых, правило деления суммы на число. После этого можно использовать метод работы с учебником. Следует обратить внимание, что здесь двузначное число заменим суммой разрядных слагаемых. При решении примера 36:2 другим приемом 36:2=(20+16):2=20:2+16:2=10+8=18, учащимся разъясняем: "36 заменим слагаемыми 20 и 16, которые разрядными числами не являются, их называют удобными слагаемыми. Этот прием нам понадобится на следующих уроках".

Прием деления вида 96:4, 70:2 можно вводить, используя проблемный метод обучения (см. гл. 4, § 8). Деления вида 60:20, 68:17 выполняется приемом подбора частного. Здесь можно использовать метод рассказа (см. гл. 4, § 3) или метод работы с учебником.

К внетабличному относятся и случаи умножения и деления:

На этом этапе также изучается проверка умножения и деления. Учащимся предлагаем пример 78:3=26 и, повторив связь между делителем и частным, составляем пример: 26·3. Решив его, мы получим 78, т.е. делимое, значит деление выполнено верно.

Деление с остатком завершает изучение умножения и деления в пределах 100.

Учащимся предлагается отсчитать 7 кружков и разложить их по 2(можно используя моделирование). Выясняем, что по 2 кружка получилось 3 раза и 1 остался. Решение записываем так: 7:2=3 (ост. 1).

В ходе выполнения упражнений на закрепление, делаем вывод, что остаток при делении всегда должен быть меньше делителя.

Используя понятие деления с остатком выполняются деления вида 23:4, где учащиеся рассуждают так: "23 не делится на 4. Самое большое число до 23, которое делится на 4, это 20. Разделим 20 на 4, получится частное 5. Вычтем 20 из 23, получится остаток 3: 23:4=5 (ост. 3). Остаток 3 меньше, чем делитель, значит деление выполнено верно".

В связи с отсутствием в учебниках формулировки некоторых правил, полезно иметь справочный материал (индивидуальную, внеклассную) следующего содержания в виде таблицы 26

Таблица 26