5. Задачи на движение

Задачи на движение вводятся в 3 классе.

Подготовительной работой является:

1) введение понятий: скорость, время и расстояние (см.гл.2,§ 6);

2) вывод правил нахождения скорости, времени и расстояния (см. гл.2, § 7);

3) решение простых задач трех видов, текст которых читатель без труда восстановит из таблицы 21:

Таблица 21

При ознакомлении с составными задачами на движение разбор задачи целесообразно вести от вопроса к числовым данным (см. § 3 этой главы), о чем мы уже подробно говорили. В 3 классе рассматриваются три вида задач на встречное движение (11, с. 239-241).

1 вид - даны скорость каждого из тел и время движения, искомое - расстояние.

З а д а ч а: Из двух поселков выехали одновременно навстречу друг другу два велосипедиста и встретились через два часа. Один ехал со скоростью 15 км/ч,а второй -18 км/ч. Найти расстояние между поселками.

Рис.82

До решения выясняют смысл числовых данных, какой из велосипедистов проедет больше расстояния и ближе к какому концу отрезка указать место встречи при построении чертежа (рис.82). Последнее после сверяется с ответом задачи. (Аналогично и в других видах задач на движение.)

Решение: 1) Сколько километров проехал 1 велосипедист?

15·2=30 (км)

2) Сколько километров проехал 2 велосипедист?

18·2=36 (км)

3) Сколько километров между поселками?

30+36=66 (км)

2 вид - даны скорость каждого из тел и расстояние, искомое - время движения (рис.83):

З а д а ч а: Расстояние между поселками - 66 км. Из них одновременно выехали два велосипедиста. Скорость первого 15 км/ч, скорость второго 18 км/ч. Через сколько часов они встретились?

Рис.83

Решение: 1) На сколько км сближаются велосипедисты за час?

15+18=33 (км)

2) Сколько времени пройдет до встречи велосипедистов?

66:33=2 (ч)

Ответ: через 2 часа.

3 вид - даны расстояние, время движения и скорость одного из тел, искомое - скорость другого тела (рис.84).

З а д а ч а: Расстояние между поселками 22 км. Одновременно навстречу друг другу вышли два пешехода. Первый шел со скоростью 6 км/ч. Через 2 часа они встретились. Найдите скорость второго пешехода?

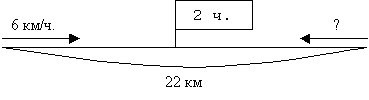
Рис.84

Решение: 1) Сколько км прошел первый пешеход до встречи?

6·2=12 (км)

2) Сколько км осталось пройти второму пешеходу?

22-12=10 (км)

3) С какой скоростью шел второй пешеход?

10:2=5 (км/ч)

Ответ: 5 км/ч

В задачах на движение в противоположных направлениях работа ведется аналогичным образом. В их краткой записи используются такие чертежи (рис.85):

Рис.85

При решении задач на движение учителю большую помощь окажет опорная схема (рис.86):

Рис. 86