2. Задачи на нахождение четвертого пропорционального

В задачах на нахождение четвертого пропорционального даются три величины, связанные с пропорциональной зависимостью (прямой, обратной) и, исходя из которых, находят четвертую, искомую величину. Эти четыре величины составляют пропорцию, отсюда и название этих задач.

Величинами в этих задачах могут быть цена, количество, стоимость; скорость, время, расстояние; масса одного предмета, количество предметов, общая масса и другие.

В методической литературе, в частности в (11, с. 226), описывается следующая классификация задач на нахождение четвертого пропорционального (таблица 19):

Таблица 19

Первые четыре задачи с прямо-пропорциональной, последние две - с обратно пропорциональной зависимостью (в чем нетрудно убедиться, составив пропорцию).

В начальной школе распространенным способом решения этих задач является способ нахождения значения постоянной величины. Например, в задаче 1 решением будет: 1) 4:2=2 (р.) - цена моркови; 2) 2·6=12 (р.) - всего уплатили.

Однако, для общего развития учащихся полезно решать эти задачи и нахождением коэффициента пропорциональности (термин для учителя - А.А.). Например, в той же задаче: 1) 6:2=3 (раза) - во столько раз больше купили моркови; 2) 4·3=12 (р.) - всего уплатили.

Задачи данного вида с величинами цена, количество и стоимость вводятся во 2 классе раньше задач с другими величинами. Рассмотрим методику работы с ними.

Подготовительная работа к решению задач на нахождение четвертого пропорционального с величинами цена, количество и стоимость начинается с ознакомления со связью между ними. Это можно провести через игру в "магазине" (прием М.И. Моро, М.А. Бантовой).

На доску прикрепляются "товары": тетради, карандаши, блокноты и т.д. На них обозначены цены (прикреплены этикетки: "Цена 3 руб.", "Цена 5 руб." и т.д.).

- Сегодня будем играть в "магазин" и решать задачи о покупках. Вот это магазин. (Показывает на доску.) Что продается в магазине? (Называют.) На вещах обозначена цена. Назовите цену тетради. (3 руб.) Цену блокнота. (5 руб.) Что же показывает цена? (Сколько стоит 1 тетрадь, 1 блокнот и т.д.) Я куплю 3 тетради. Что обозначает число 3? (Сколько вы купили тетрадей.) Иначе говорят: это число тетрадей, или количество тетрадей. Я купила 8 блокнотов. Что обозначает число 8? (Число блокнотов или количество блокнотов.) Сколько денег я должна уплатить за 2 блокнота? (10 руб.) Как вы узнали? (5 2=10.) 10 руб. – это стоимость 2 блокнотов.

На доске в таблице учитель записывает:

            Далее один из учеников назначается продавцом, а несколько учеников - покупателями. Покупатели по очереди подходят к продавцу и покупают несколько вещей. Ученики из класса составляют задачи на эти покупки, решают их и записывают в таблице. После решения 2-3 задач учащиеся делают вывод: если известны цена и количество, то можно найти стоимость, умножив цену на количество.

На других уроках решаются простые задачи на нахождение цены, количества по известным двум другим величинам. Для работы у доски учителю очень удобна опорная схема (рис.78).

Рис.78

            При ознакомлении с задачами данного вида учителю сразу следует начинать приучать учащихся к разбору от вопроса к числовым данным, используя графическую схему. В задаче 1 таблицы это выглядит так (рис. 79):

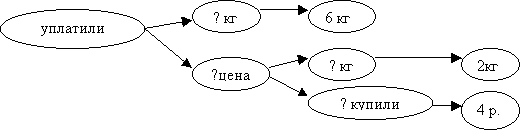
Рис. 79

Запись решения таких вначале выполняется по действиям с пояснениями, а после по указанию учителя.

При закреплении решения этих задач полезно показать и другой способ их решения (через коэффициент пропорциональности - термин учащимся не сообщается). Для закрепления далее постепенно вводятся аналогичные задачи с другими величинами. Используются различные ранее рассмотренные нами приемы закрепления.