3. Методика работы над задачами на усвоение конкретного смысла арифметических действий

Задачи на нахождение суммы и остатка вводятся одновременно, поскольку одновременно вводятся действия сложения и вычитания. Это не только способствует развитию умения решать задачи, но и развивает, в частности, обратимость мышления.

Подготовкой к решению задач на нахождение суммы и остатка является выполнение операций над множествами: объединение конечных непересекающихся множеств (связь со сложением) и удаление из данного множества его подмножества (связь с вычитанием). Упражнения на операции с множествами включаются в подготовительный период и при изучении нумерации чисел в пределах 10. Они, в основном, выполняются практически с предметами. Например, при введении знака "+" учащимся предлагают положить перед собой 2 предмета и чуть в сторону 1 предмет. Просим их "собрать в кучу" и сообщаем, что мы выполнили сложение: к 2 прибавили 1, 2 увеличили на 1 и т.д. После этого знакомим со знаком "+" и записью 2+1=3. Учащиеся должны четко представить, что при сложении происходит увеличение числа предметов.

Аналогичная подготовительная работа к решению задач на нахождение остатка проводится при ознакомлении со знаком «-«. Сами термины "сложение" и "вычитание" в учебнике вводятся позднее, но такое опережающее их введение не приводит к перегрузке учащихся и способствует развитию математической речи.

Такие упражнения продолжаются и на других уроках. В целях развития математической речи и умения составлять задачи надо требовать от учащихся краткого описания своих действий: "У меня было 5 кружков. Я положил еще 1 и их стало 6. Поэтому 5+1=6".

Ознакомление с решением задачи на нахождение суммы и остатка начинается с составления задачи по такой же методике, как и при первоначальном ознакомлении с задачей. После решения составленных задач работают по тексту задач в учебнике, где одновременно предлагаются задачи (Моро М.И. и др. Математика, 1 кл., 1995, с. 57):

После восприятия и осмысления каждой задачи выполняем одновременно их модели (рис. 62),

Рис.62

записываем решения а) 6+4=10 (билетов, б) 10-6=4 (билета) и выясняем, почему в одном случае решаем сложением (собрали в "кучу"), а в другом случае вычитанием (удаляем ту часть, где написано число 6, остается меньше, поэтому вычитаем). Учащимся говорим, что первая задача – это задача на нахождение суммы, а вторая - на нахождение остатка. Умение определять вид задачи не является для учащихся обязательным. Но все же, умеющим определить вид задачи, легко представить ее модель в воображении и решить задачу иногда устно. Имея "в голове" воображаемую модель, учащийся более грамотно рассуждает и объясняет.

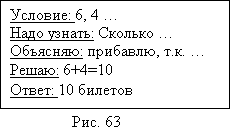
В первое время при решении задач учащиеся затрудняются четко выделить условие и вопрос задачи, при повторении работы над задачей ответ тоже включают в число данных. Чтобы избежать этих затруднений нужна полноценная работа над восприятием и осмыслением задачи, чередуя различные приемы, в том числе и моделирования. Очень полезны учащимся такие опорные схемы (рис.63), используемые как памятки.

Сначала их читает сам учитель, дети отвечают, далее дети читают сами и отвечают. Числа и надписи учитель готовит сам в виде разрезных цифр, слов и по мере необходимости вставляет их в кармашки. Они могут быть использованы и для составления задач.

При закреплении учитель подбирает достаточное число задач как для устного счета, так и для письменного решения. Постепенно эти задачи входят в составные задачи, решаемые позже.

На этом этапе полезно чередовать разные приемы моделирования, что развивает гибкость мышления и внедрять приемы работы, используемые на этапе закрепления.

Задачи на нахождение суммы одинаковых слагаемых вводятся во 2 классе при раскрытии конкретного смысла умножения.

Подготовительная работа к введению этих задач начинается в 1 классе решением задач на нахождение суммы одинаковых слагаемых выполнением действия сложения. Во 2 классе предлагаются задания:

1) Нарисуй 4 раза по 2 флажка; 2 раза по 4 флажка.

2) В каждом пакете по 10 кубиков. Сколько кубиков в 3 пакетах? 4 пакетах?, которые, используя рисунок, решаются сложением. Учителю надо обратить внимание учащихся на выражение: "в каждом" - в первом пакете 10 кубиков, во втором пакете 10 кубиков, в третьем пакете 10 кубиков. Решение записывают так: 10+10+10=30 (кубиков) и т.д.

Ознакомление с задачей на нахождение суммы одинаковых слагаемых осуществляется через задачу типа: "Сделай по задаче рисунок и реши ее: "На каждой тарелке 5 яблок. Сколько яблок на трех тарелках?". Учащиеся рисуют модель задачи (рис.64) и записывают: 5+5+5=15 (яблок), 5·3=15 (яблок).

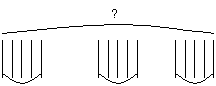
Рис.64

Такой двойной записью следует пользоваться дольше, чтобы не произошло преждевременное сокращение процесса рассуждения. В этом случае учащиеся лучше усваивают смысл каждого компонента умножения: 5 – это слагаемые, а 3 - показывает, сколько таких равных слагаемых.

При закреплении решения задач данного вида вводятся задачи с величинами: цена, количество и стоимость (2 класс), скорость, время и расстояние (3 класс). Методику работы с ними рассмотрим в § 8 этой главы.

Задачи на деление по содержанию вводятся в связи с изучением деления во 2 классе.

Подготовительная работа начинается в 1 классе устными упражнения вида: "Мальчики разделили 8 мячей, по 2 мяча каждому. Сколько мальчиков получили мячи?". Их решают, пользуясь наглядными пособиями: вместо мячей берут кружки и проделывают с ними то, что сказано в содержании задачи (здесь - разбивают по 2 в группы и получают в ответе 3).Полезно уже на данном этапе вводить моделирование (рис.65), что способствует развитию умений абстрагировать, использовать аналогию и т.д. Такие упражнения продолжаются и во 2 классе до введения деления.

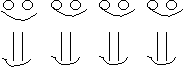
Рис. 65

Выполняя эти упражнения, учащиеся должны понимать, что мячи и т.п. дети получили поровну.

Для ознакомления с задачей на деление по содержанию учащимся предлагается задача: "У бабушки было 10 морковок. Она связала их в пучки по 5 морковок. Сколько получилось пучков?". Решение сначала учащиеся объясняют по рисунку учебника. После этого все это дублируют своими кружками.

- Вместо морковок в задаче возьмите и положите на парту кружки (кладут 10 кружков). Теперь что сделаем? (Положим их в кучи.) По сколько кружков положите в кучи? (По 5.) Что вы сделали с 10 кружками? (Разложили их в кучи или разделили на кучи.) Какое это действие нам подсказывает для записи решения? (Деление.) Запишем. (10:5=2 (пучка)). Что означает число 2? (Это значит 5 кружков получилось 2 раза.) Хорошо, а если проделаем обратно: соберем эти кружки снова в одну кучу, что мы получим? (10 кружков.) А в задаче? (10 морковок.) Проверим.

Далее записываем модель задачи аналогичный рисунку 65. Устную проверку таких задач проводят с целью отработки приема классификации и формирования навыков проверки решения через обратную задачу.

При закреплении умения решать задачи на деление по содержанию учащиеся постоянно повторяют рассуждения вида: "10 кружков разложили (раздали, разделили и т.д.) по 5 кружков поровну, получилось 2 (кучи, группы и т.д.); значит 10:5=2" с постепенным переходом к сокращению: про себя повторяют - "10 кружков разложили...", а вслух говорят - 10:5=2.

Задачи на деление на равные части вводятся во 2 классе тоже в связи с изучением деления.

В качестве подготовительной работы в 1 классе рассматриваются упражнения вида: "Разложи 8 карандашей в 2 коробки поровну. Сколько карандашей в каждой коробке?", которые решаются используя предметные модели или рисунки. Изображение решения в виде модели на данном этапе нецелесообразно из-за другой последовательности действий их составления.

Такие упражнения продолжаются во 2 классе до введения деления.

Ознакомление с задачами на деление на равные части можно осуществить, используя задачу: "Возьми из набора 6 кружков и разложи их на 2 равные части. По сколько кружков в каждой части?" По аналогии с задачами на деление по содержанию, они могут начать раскладывать их по 2 и получить неправильное решение: получили 3 части и по 2 в каждой, значит ответом будет 2 кружка. Чтобы этого не произошло, учащиеся должны работать строго дублируя действия учителя.

- Мы с вами сегодня учимся решать задачи нового вида на деление: деление на равные части. Вы должны делать только то, что я буду делать. Возьмите каждый в руки 6 кружков. Нам их надо разложить на 2 равные части. Обратите внимание: не по 2, а на 2 равные части. Выделим сначала эти части: на наборном полотне первая строка будет одной частью, вторая строка - второй частью. У вас на партах место слева - одна часть, место справа - другая часть (если у них нет наборного полотна - А.А.). Положим на

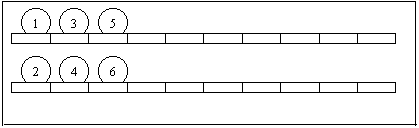
Рис. 66

полотно в каждую часть по одному кружку. (Учащиеся делают на партах.) Теперь положим еще по одному и у нас стало…(стало 2) Теперь положим еще по одному (рис. 66 - номера кружков показывают последовательность их размещения). Все кружки мы разложили? (Все.) Сколько кружков в каждой части? (3 кружка.) Одинаковое или разное число? (Их поровну.) Мы разложили 6 кружков на 2 равные части и получили 3. Задача решается делением и записывается 6:2=3 (кружка). Теперь нарисуем модель задачи. Дугами покажем 2 равные части (Чертят в тетради.) Нарисуем в каждой части по одной палочке, пусть они

 изображают кружки. Теперь нарисуем еще по одной.

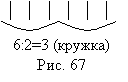Сколько мы нарисовали? (4 палочки.) Осталось еще… (2 палочки.) Нарисуем их. Сколько палочек в каждой части? (3 палочки.) Запишем под рисунком решение (рис. 67)

При закреплении решения задач данного вида учащиеся отрабатывают рассуждение вида: "положим по одной палочке в каждую часть, потом еще по одной и т.д.".

Далее, одновременно рассматривая задачи на оба вида деления, уточняем, что: если сказано "разложить по 4", то сначала рисуем все палочки и каждые 4 палочки показываем дугой; если сказано "разложить на 4 равные части", то сначала рисуем 4 дуги и разложим палочки по одной в каждой, еже раз по одной и т.д., пока не кончатся палочки. Учащиеся должны усвоить не просто решение, а, прежде всего, технологию разбиения множества на непересекающиеся подмножества, при котором в одном случае находим число элементов подмножества (деление на равные части), а в другом число подмножеств (деление по содержанию).