§ 3. Поиск плана решения задачи

Поиск плана решения фактически начинается на этапе моделирования. Некоторые учащиеся уже находят решение, т.е. они уже знают, какие действия надо выполнить, чтобы решить задачу. Однако, часть детей без помощи учителя этим не справляется. Поэтому для них нужна специальная беседа, которая называется разбором задачи.

Разбор задачи - это выявление зависимостей между данными величинами, между искомой величиной и данными, расчленение задачи на основе этих зависимостей на более простые и установление последовательности их решения для получения ответа на вопрос задачи (составление плана решения).

При ознакомлении с новым видом простых задач учитель сам ведет разбор, учащиеся отвечают на вопросы.

Например, при разборе задачи: "У Коли 8 марок, а у Шуры на 2 меньше. Сколько марок у Шуры?" - целесообразно поставить такие вопросы: Что требуется узнать в задаче? (Сколько марок у Шуры.) А их было больше или меньше, чем у Коли? (Меньше, потому, что сказано, что у Шуры марок на 2 меньше.) Если меньше, то каким действием решается задача? (Вычитанием.) Далее выполняется решение. Если же при разборе работаем по модели, то сначала рассуждения ведутся на "языке модели": "У Шуры кружков больше или меньше?", "Отрезок, показывающий марки Шуры, короче или длиннее?" и после этого снова повторяем со словом "марки".

При ознакомлении с новым видом составных задач рассуждения ведутся аналогично. Здесь учащиеся накапливают опыт осуществления разбора по указаниям учителя. Разбор составной задачи заканчивается составлением плана решения. Учитель, переходя к специальному знакомству учащихся с разбором задачи, знакомит их с одним из видов рассуждений: от вопроса задачи к числовым данным или же от числовых данных к вопросу. Это может быть сделано без построения графических схем или же с построением.

1. Разбор задачи рассуждением от вопроса к числовым данным.

Этот способ основан на анализе и в методической литературе можно встретить другое название - "аналитический способ разбора задачи". При разборе задачи от вопроса к числовым данным рассматриваемый вопрос мысленно расчленяется на другие вопросы, каждый из которых затем рассматривается в отдельности. В случае необходимости они, в свою очередь, расчленяются опять на другие вопросы и до тех пор, пока мы не придем к исходным данным задачи.

З а д а ч а. Из двух городов А и В вышли навстречу друг другу одновременно два поезда. Один шел со скоростью 50 км/ч, другой - 60 км/ч. Какое расстояние между городами, если до встречи они шли 4 часа?

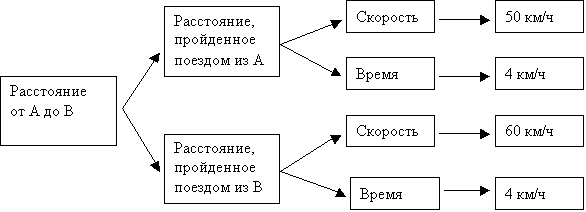
Рассмотрим данный способ разбора, где рассуждения поэтапно изобразим в виде графической схемы (поэтапно изобразив рассуждения графически, получим схему на рис. 57). Что требуется узнать в задаче? (Расстояние между городами А и В.) Можно ли это узнать сразу? (Нет.) Что надо знать, чтобы найти расстояние от А до В? (Надо знать расстояние, пройденное каждым поездом до встречи.) Знаем ли расстояние, пройденное поездом из А? (Нет.) Что для этого надо знать? (Его скорость и время движения.) Знаем ли мы их? (Да, скорость 50 км/ч, время движения 4 ч.) Значит, сможем мы найти расстояние, пройденное поездом из А? (Да.) Известно ли расстояние, пройденное поездом из В? (Нет.) Что надо знать, чтобы его найти? (Скорость и время движения.) Знаем ли мы их? (Да, скорость 60 км/ч, время движения 4 ч.) Сможем ли мы теперь найти это расстояние? (Да.) Теперь составим план решения. Что мы найдем первым? (Расстояние, пройденное поездом из А.) Каким действием? (Умножим скорость на время.) Что найдем после этого? (Расстояние, пройденное поездом из В.) Каким действием? (Так же.) Что узнаем дальше? (Расстояние между городами.) Каким действием? (Сложением.) Ответим ли мы на вопрос задачи? (Да.)

Рассуждение от вопроса к числовым данным представляет логическую цепь заключений, органически связанных между собой и поэтому оно хорошо развивает логическое мышление учащихся. Этот способ более целенаправлен на составление плана решения, т.к. ученик видит все рассуждение в целом.

В системе развивающего обучения предпочтение отдается этому способу разбора задачи.

Рис. 57

2. Разбор задачи рассуждением от числовых данных к вопросу.

Этот способ основан на синтезе и поэтому в методической литературе называют еще синтетическим методом разбора задачи.

Рассмотрим разбор той же задачи данным способом (Поэтапно изобразив рассуждения графически, получим в конце схему на рис.58).

Что нам известно в задаче о поезде из города А? (Его скорость 50 км/ч, время движения 4 ч.) Что мы можем найти по этим данным? (Расстояние, которое он прошел.) Каким действием? (Умножением.) О поезде из В что мы знаем? (Скорость 60 км/ч, время движения 4 ч.) Что можем найти по этим данным и каким действием? (Расстояние, умножением.) Мы будем знать расстояние, пройденное каждым поездом до встречи. Что мы тогда сможем найти? (Расстояние между городами А и В.) Каким действием? (Сложением.) Ответим ли мы на вопрос задачи? (Да.)

После этого аналогично составляется план решения задачи:

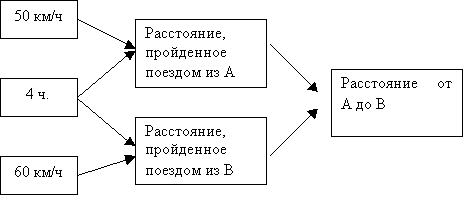
Рис. 58

Этот способ разбора менее эффективен, т.к. он направлен на выбор действия, который может оказаться и ненужный. Например, используя 60 км/ч и 50 км/ч, ученик может выполнить вычитание: 60-50=10 (км/ч), которое в задаче совершенно не нужно.

Графические схемы рассуждений представляют из себя схему самого процесса мысли, т.е. ученик наглядно видит движение мысли и результаты мыслительных операций. Обучению учащихся к построению таких схем следует начинать при введении составных задач в два действия. Постепенно у них развиваются навыки самостоятельного их составления.

Более подробно с методикой использования графических схем можно познакомиться в работе (72).