§9 Интегральная технология обучения

Среди различных технологий обучения одним из эффективных технологий является интегральная технология обучения. В старших классах она находит применение, а в начальных классах - пока пробивает дорогу. Применяя эту технологию, учитель должен иметь, прежде всего, четкое о ней представление. Поэтому еще раз уточним понятие "интегральная технология".

Основой данного термина служит слово "интеграция", которая понимается: 1) объединение в целое каких-либо частей, элементов; 2) экономический процесс взаимного приспособления и объединения национальных хозяйств двух и более государств с однотипным государственным строем. В практику обучения часто переносят второе понимание термина "интеграция" и отсюда интегрированные уроки ( математика + труд и т д.) и интегрированные программы. Несомненно, они приносят пользу, поскольку в их основу положены межпредметные связи.

Если же в основу взять термин в первом понимании применительно к одному предмету, то можно говорить об интегральной технологии в рамках этого предмета.

Справедливо отмечает В.В.Гузеев: "Анализ методологической, педагогической, научно-методической, психологической литературы показывает, что наиболее перспективной считаются четыре направления, вокруг которых и группируются большей частью работы: укрупнение дидактических единиц, планирование результатов обучения, психологизация образовательного процесса, компьютеризация.

В каждом из указанных направлений есть определенные достижения. Естественно предположить, что если удастся сплавить эти направления в нечто единое, целостное, интегральное, то результатом может оказаться мощная технология. Эта технология и называется интегральной" (27, с.89). В этой технологии укрупнение дидактических единиц усвоения предполагает одновременное изучение сходных понятий (прием обобщения). Ниже мы рассмотрим блок уроков по математике в 1-м классе с учетом первых трех названных частей интегральной технологии (Для успешного усвоения нужно иметь при себе учебник.)

Сложение чисел с переходом через десяток в учебнике рассматривается в течение 9 уроков (Моро М.И. и др. Математика-1, Просвещение, 1995.-С. 81-89): на первом уроке дополнение чисел до 10, на втором - сложение, где в сумме получается число 11, на втором - число 12 и т д. Все это завершается составлением таблицы сложения. Используя интегральную технологию обучения структуру данной системы уроков можно представить в такой форме.

Предварительно поясним, в чем заключается содержание вышеназванных направлений как частей интегральной технологии.

Укрупнение дидактической единицы усвоения заключается:

1) в совместном и одновременно изучении взаимосвязанных примеров вида 9+4, 6+5, 7+7 и т.д. на 1-м уроке, обладающих информационной общностью (в основе лежит один и тот же принцип действия);

2) в обеспечении единства процессов составления и решения задач (3-´ урок);      

3) в достижении системности знаний при сложении с переходом через десяток.

Планирование результатов обучения заключается:

1) в достижении усвоения состава числа 10 при вводном повторении;

2) в планировании и овладении минимальным уровнем знаний при первичном закреплении на 1-м уроке и дополнительном закреплении на 2-м;

3) в подборе целесообразных задач с целью закрепления вычислительных приемов;

4) в обобщающем повторении в связи с подготовкой к проверочной работе на 7-м уроке.

Психологизация образовательного процесса заключается:

1) в использовании приема укрупнения дидактической единицы усвоения;

2) в определении главного действия (дополнение числа до 10) после повторения состава числа 10 при вводном повторении;

3) в действии учителя, при котором преднамеренно создается затруднение (проблемная ситуация) в работе с наборным полотном, т.е. возникают потребности в нахождении нового приема вычисления (1-´ урок);

4) в определении рационального способа действия и в организации работы над запоминанием основного рассуждения (1-й урок);

5) в использовании приема целесообразных задач, где ранее приобретенные знания используются в новой ситуации, т.е. учащиеся «переводятся» на уровень творческого задания;

6) в осуществлении развивающе-дифференцированного обучения на 406 уроках;

7) в использовании заданий для развития различных компонентов математических способностей учащихся;

8) в использовании коррекции знаний, при котором учащиеся сами исправляют свои ошибки («доработка» своей работы).

Компьютеризация обучения означает работу учащихся на компьютерах по специально составленным по данной теме программам. Этот вопрос в начальных классах в массовой школе ждет еще своего решения.

Т е м а: Сложение чисел с переходом через десяток.

1-й урок - урок изучения нового материала.

1.Вводное повторение (ВП). Повторяют состав чисел от 2 до 9 (устно) под руководством учителя. На этом этапе учащимся предлагаются задания типа: "Дополни до 10 числа 9,8,7,6,5,4,3,2" (см. учебник), что является основным принципом при сложении с переходом через десяток.

В конце повторения учитель делает вывод: "Ребята! Вы все усвоили состав чисел от 2 до 9, умеете дополнять число до 10. Все это нам понадобится при изучении сложения с переходом через десяток. Как вы думаете, например, при решении примера 9+4 какое наше действие будет главным? (Дополнение числа 9 до 10.)" Если нет ответа, эта цель устанавливается в ходе изучения новой темы. Одна из целей - сложение с переходом через десяток - уже поставлена и поэтому можно приступить к дальнейшей работе. В данном случае мы поставили цели урока с предварительным диагнозом уровня ранее приобретенных знаний (выяснили знание состава чисел, таблицы сложения в пределах 10).

2. Изучение нового материала. Учащимся предлагается решить пример 9+4, используя наборное полотно. Основную роль при этом играет учитель, т.к. главной задачей является усвоение принципа сложения. Работа на наборном полотне организуется следующим образом.

На доске вывешивается наборное полотно (обязательно с десятью кармашками в два ряда) и проводится беседа:

- Ребята, что значит к 9 прибавить 4 "на языке" кружков? (К 9 кружкам надо положить 4 кружка.)

- Кто это сделает? (Идет к доске ученик.) Учитель при этом мешает ему положить кружки в нижний ряд ("нечаянно" закрывает этот ряд или по "невнимательности" вешает туда другой плакат и т.п.) и вынуждает ученика положить в верхний ряд один кружок. Если так не сделать, то ученик, как правило, кладет все 4 кружка в нижний ряд и при этом исчезает принцип сложения, т.е. сложение сводится к подсчету числа кружков до 13.

- Почему ты положил 1 кружок в верхний ряд, а не все сразу в нижний ряд? (Вы мешали работать.)

- Хорошо, не буду мешать (открывает нижний ряд). Далее что сделаешь? (Положу 3 кружка.)

- Теперь расскажи наши действия одновременно кружками и числами.

К 9 кружкам положили 1 кружок... (К 9 прибавили 1...), получилось 10 кружков... (получилось 10...), потом к 10 кружкам положили 3 кружка... (к 10 прибавили 3) и получилось 13 кружков... (получилось 13). Запишем решение:

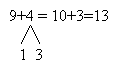
- Хорошо. А могли бы мы к 9 кружкам положить сначала 2 кружка, если бы нижний ряд был закрыть? (Нет, кармашек наверху не хватит.)

- А что надо сделать, чтобы хватило? (Надо еще кармашки добавить.)

- А это удобно? (Нет.)

- Значит, как удобнее? (Как в первом случае.)

- То есть, к 9 можно сначала прибавить 2, а потом еще 2, но это... (Неудобно.) Удобно... (Сначала прибавить 1, а потом 3.)

- Что мы сделали, прибавив к 9 единицу? (Дополнили до 10.)

- Потом прибавили 3 и получили 13. От 9 мы к какому числу перешли? (к 13). При этом через какое число переходили? (через 10). Значит, у нас получилось сложение с ...(переходом через десяток). Сделаем главный вывод: чтобы выполнить сложение с переходом через десяток, надо число... (дополнить до 10) и потом (прибавить оставшееся число).

Далее учащиеся хором, а потом индивидуально повторяют это рассуждение, что необходимо для его запоминания. У слабых учащихся запоминание улучшается при повторении примера разными сюжетами: "чтобы к 9 куклам прибавить 4 куклы,...", "чтобы к 9 машинам положить 4 машины,..." и т.п., т.е. теми предметами, что у кого дома есть (Здесь мы имеем дело с элементами образного мышления). После этого учитель предлагает разобраться с примерами 6+5, 8+4, 7+7 и т.д.(по одному примеру с каждой последующей страницы). При этом все время внимание учащихся акцентируется на принципе сложения. Надо помнить, что при интегральной технологии на одном уроке рассматривают несколько тем, основой которых является один и тот же принцип действия.

3.Первичное закрепление. При закреплении на этом уроке с каждой страницы (с 81 по 86) рассматриваются по 2-4 примера (примеры до красной рамки). Если позволяет время, то можно решить все эти примеры.

2-й урок-закрепление (З) На данном уроке рассматриваются все оставшиеся примеры учебника, приведенные до задач: №3(с.81), №4(с.82), №3(с.83), N4(с.84),N3(с.85-87),N5(с.88,89). Также заполняются таблицы в правом верхнем углу страниц. Работа завершается составлением таблицы сложения. Словом, на этом уроке учащиеся должны овладеть минимальным уровнем знаний (все до единого!). На этом же уроке учащиеся постепенно переходят к самостоятельной работе под наблюдением учителя.

3-й урок - изучение нового материала (дополнительный объем) (ИНМ(ДО)).

Урок посвящается решению задач (N1,2-с.81, N1-с.82,83,85), связанных с изученной темой. Прежде всего рассматриваются задачи на сложение, но при этом задачи учебника заменяются целесообразными задачами. Например, задачу "Вова поступил в школу в 7 лет и окончил её через 10 лет. Сколько лет ему было, когда он окончил школу?" целесообразно заменить задачей : "Вова поступил в неполную среднюю школу в 7 лет и окончил её через 8 лет. Сколько лет ему было, когда он окончил школу?", т.к. её решение 7+8 связано с изучаемой темой. Словом, сюжет задачи остается тем же, но меняются только данные ("подгоняем" к сложению с переходом через десяток). Важно, чтобы учащиеся поняли цель такой замены, т.е. должна быть мотивация. При её

 отсутствии они просто окажутся в недоумении. Если позволяет время, то могут быть решены и другие задачи.

4-6 уроки. На этих уроках осуществляется развивающее дифференцированное обучение (РДО). Часть учащихся на уроке объединяется в группы, и каждая группа получает задание на ограниченное время, по истечении которого группа отчитывается о своей работе в той или иной форме. В нашем случае группы работают над оставшимися задачами, примерами на с.81-89 и дополнительно получают примеры на сложение с переходом через десяток. После оценки работы группы её участники получают одинаковые баллы. Если на группы разбит не весь класс, то во время работы имеющихся групп учитель занимается с остальными учащимися. Сюда входят, как правило, более слабые и они образуют как бы группу выравнивания. Вариантов таких форм работы много и всё зависит от профессиональной подготовки учителя. На этих же уроках могут быть использованы различные упражнения на развитие математических способностей.

7-й урок - урок обобщающего повторения и подготовки к проверочной работе (ОП). Составляется таблица сложения как на с.89, подбираются примеры на сложение с переходом через десяток в одно и два действия, простые и составные задачи, аналогичные решенным. Обращается внимание на затруднения учащихся, выявленные на предыдущих уроках.

8-й урок - контроль усвоения (КУ), который проводится в форме самостоятельной работы. Текст предлагается на различных уровнях:

1) На оценку "3" (минимум) -2 простые задачи на сложение и вычитание, 8 примеров на сложение с переходом через десяток и два-три примера в два действия.

2) На оценку "4" - 1 простая задача с отношениями "на больше" (1-й вариант) и "на меньше"(2-й вариант),1 составная задача, 4 примера на сложение с переходом через десяток, 2 примера в два действия.

3) На оценку "5" - 2 составные задачи на сложение и вычитание, 8 примеров на сложение с переходом через десяток, 2 примера в два действия.

Объём заданий определяется с учётом уровня знаний учащихся. При этом минимальный уровень знаний должен быть достигнут всеми учащимися.

9-й урок- урок коррекции знаний (Кор), т.е. работа над ошибками. В идеальном варианте учитель должен вернуть работы учащихся без исправлений ошибок, с подчёркиванием тех мест, где они есть. Учащиеся же сами должны их исправить под руководством учителя. В зависимости от психологических особенностей учащихся учитель может разрешить некоторым из них пересдачу.

 Как видим, блок уроков при интегральной технологии обучения можно представить в виде нижеследующей таблицы 17 (УДЕ - укрупнение дидактической единицы, ПРО - планирование результатов обучения, ПсО - психологизация обучения):

Таблица 17

Используя данную технологию в 1-м классе, можно изучить такие темы, как "Вычитание вида 12-5 (с.93-103)", "Прибавление числа к сумме и вычитание числа из суммы: (4+3)+2, (4+3)-2, 34+20, 34+2, 48-30, 48-3, 26+4, 30-6 (с.122-132)" и другие.

В заключение отметим, что интегральная технология, осуществляемая внутри одного предмета, доступна большинству учителей и даёт, как правило, более высокие результаты. В то же время, под видом данной технологии нельзя изучать одновременно вопросы, не имеющие в основе общих принципов. В этом случае интегральной технологии просто не будет.