§ 7. Алгоритмический метод обучения

В процессе обучения учитель должен научить учащихся объяснять свое решение примера или задачи (с места, у доски и т.д.). Это возможно в том случае, если он не только предлагает учащимся образцы ответов, но требует строгого их соблюдения. Если образцы ответов предлагаются в виде алгоритма, т.е. списка конкретных указаний, то в этом случае мы имеем дело с алгоритмическим методом обучения.

Я.И. Груденов для успешного использования алгоритмического метода предлагает соблюдать следующие условия (26, с. 65-67): 1) алгоритмический метод необходимо сочетать с применением образца ответа, для чего алгоритм должен быть удобным для применения; 2) алгоритм по возможности должен быть наиболее кратким, т.е. возможным для запоминания; 3) при использовании алгоритма от учителя требуется постоянная установка типа: "Читая и применяя алгоритм, старайтесь запоминать его"; 4) учитель сам должен пунктуально соблюдать образцы применения алгоритма; 5) в алгоритм желательно включать указания, побуждающие учащихся контролировать свои действия; 6) указания в алгоритме желательно давать в таком виде, чтобы они содержали в себе все необходимые объяснения, какие учитель хочет слышать от учащихся по ходу решения примера или задачи.

В методической литературе описываются различные виды алгоритмов. В начальной школе наиболее часто встречаются алгоритмы-описания и алгоритмы-схемы.

Алгоритм-описание - это перечень и конкретный показ операций, входящих в вычислительный прием, математическое свойство и т.п. Примером таких алгоритмов являются приводимые в учебниках начальных классов объяснения сложения, вычитания, умножения и деления столбиком.

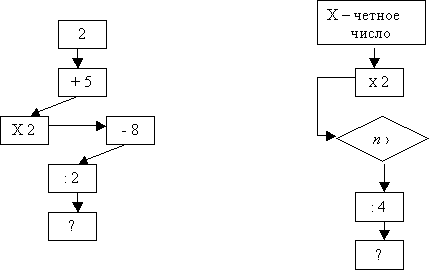
Алгоритм-схема - это перечень и показ операций в виде различных схем, в частности, блок-схем. Примерами таких алгоритмов являются схемы на рис.52:

Рис.52

Следует согласиться с тем, что "обучение алгоритмам - важнейшее средство развития математического мышления: усваивая алгоритмы, осуществляя перенос их в новые условия, дети учатся всесторонне анализировать математический материал, синтезировать и обобщать его по существенным признакам; в процессе алгоритмической деятельности формируются умения осуществлять переход от развернутых математических рассуждения к свернутым и обратно, с прямого хода мысли на обратный" (33, с. 69).

Учителю очень важно построить обучение так, чтобы учащиеся изучаемый алгоритм, где это возможно, составляли самостоятельно под его руководством. Если же они часто будут обучаться готовым алгоритмам, возникает опасность формализма, шаблонов, нетворческого подхода к решению примеров и задач.

Алгоритмический метод в сочетании с другими методами обучения (метод целесообразных задач, проблемное обучение и др.) повышает осмысленность усвоения, облегчает и ускоряет изучение программного материала.

Рассмотрим организацию деятельности учащихся по овладению с алгоритмом в сочетании с методом целесообразных задач на примере темы "Умножение двузначного числа на однозначное" (Моро М.И., Бантова М.А. Математика, 2 кл.,1997г., с.127), где изучается решение примеров вида 23·4=(20+3)·4=20·4+3·4=80+12=92 (таблица 11).

Таблица 11

Одним из вариантов применения алгоритмического метода является использование различных памяток. При работе с памятками нужно соблюдать два важных условия: 1) памятка висит на стене или же находится на рабочем столе ученика; 2) содержание памятки дублируется учащимися до запоминания и формирования соответствующей привычки рассуждения.

Отметим, что без полного запоминания алгоритма (хотя бы со своими формулировками) алгоритмический метод не даст ожидаемых результатов.