§ 5. Развитие математической памяти.

Под математической памятью надо понимать способность человека запоминать математические объекты, понятия, отношения, рассуждения, действия и т.п. и воспроизвести их в необходимый момент. Без достаточно развитой математической памяти не может быть успешного изучения математики. Это можно подтвердить хотя бы следующим положением. Мышление на уроках математики, как функция мозга, предполагает оперирование математическими понятиями, представлениями, отношениями и т.д. А это возможно только в том случае, если последние сохранились в памяти.

Как известно из курса психологии, процесс запоминания протекает в трех формах: запечатление, непроизвольное запоминание. Произвольное запоминание. Зная это, учителю в процессе обучения необходимо учитывать некоторые закономерности запоминания:1) запоминание зависит от цели, которую поставил перед собой ученик; 2) запоминание зависит от способа и средства предъявления материала (в начальных классах - прежде всего от использования наглядности); 3) запоминание зависит от логической структуры изучаемого материала. Иногда изучение вопроса в той последовательности, как он изложен в учебнике, может оказаться менее эффективным, чем вариант изложения вопроса самим учителем; 4) запоминание зависит от рациональной организации повторения материала; 5) в запоминании должны участвовать все виды памяти: зрительная, слуховая, двигательная; 6) в процессе запоминания большую роль играет самоконтроль: воспроизведение вслух, записями, рисунками, ответы на поставленные вопросы, вопросы самому себе и ответы на них и т.п.; 7) для улучшения запоминания полезно применять некоторые специальные приемы (см. ниже).

В процессе обучения одной из важных задач учителя является систематическая и целенаправленная работа по развитию памяти учащихся. Причем работа должна быть направлена не просто запоминанию определенного количества фактов, а, прежде всего, обучению приемам рационального запоминания с должной их мотивацией. Рассмотрим некоторые приемы, способствующие более рациональному запоминанию и повышающие его результативность.

Я.И. Груденов рассматривает такие приемы мыслительной деятельности, которые одновременно являются и приемами запоминания: 1) прием мысленного составления плана; 2) прием соотнесения; 3) прием реконструкции; 4) прием использования стимулирующих звеньев; 5) прием выделения смысловых опорных пунктов (26, с. 188-195).

1. Прием мысленного составления плана - составление плана в устной форме в процессе изучения материала. Это может быть составление плана наблюдения, плана решения задачи, примера и т.п. К данному приему относится также повторение перед решением примеров правил нахождения неизвестных компонентов действий, порядка действий. алгоритма вычисления и другие. В дальнейшем ученик должен работать в соответствии с составленным планом. Все это приводит к более внимательному изучению материала и к лучшему пониманию, следовательно и к лучшему запоминанию.

2. Одним из способов улучшения понимания и запоминания является соотнесение изучаемого материала с ранее изученным. Данный прием называют приемом соотнесения.

Рассмотрим некоторые примеры.

1) Изучение приема вычисления вида 42-5 соотносится с ранее изученным приемом 47+5 (см. аналогию). При этом самое главное: учащиеся должны понять, что при переходе от примера 47+5 к примеру 42-5 сохраняются принципы действия; "доведение" до разрядного числа, сложение и вычитание, используя состав числа 5. Отличие только в действиях: в одном случае сложение, а в другом - вычитание.

2) Изучение темы "Сложение и вычитание разрядных чисел (40+20, 50-30) в 1 классе, используя прием соотнесения можно провести так.

-                 Нам надо выполнить сложение 40+20. Нельзя ли этот пример свести к сложению 4 и 2, что мы уже умеем? (Можно, если 40 представить как 4 десятка, а 20 как 2 десятка.) Какой пример мы получим в этом случае?

(4 дес.+2 дес.=6 дес.) Теперь запишем 4 десятка и 2 десятка своими обозначениями и получим пример... (40+20=60).

Аналогично рассматривается вычитание 50-30.

Прием соотнесения является одним из видов аналогии – аналогии действия. При этом на основе изучения ранее известного примера 4+2 выводится способ решения изучаемого примера 40+20.

3. Прием реконструкции - преднамеренное равносильное, т.е. без искажения, изменение изучения необходимого для запоминания материала. Это может быть изменение порядка объяснения темы урока, изменение решаемой задачи, примера и т.д. Эти изменения в конечном итоге должны привести к тому же результату, который мы должны были получить и до реконструкции.

Одним из примеров применения приема реконструкции служит сочетание компактного и раздельного методов изучения математических предложений. При компактном методе изучается часть теории и выполняются упражнения, потом следующая часть теории и упражнения и т.д. При раздельном методе сначала изучается вся теория, потом выполняются упражнения. Конкретные примеры приводятся в главе 5, § 2. Другими случаями реконструкции являются обобщение материала, его конкретизация, поиск других вариантов объяснений и обоснований, формулировка некоторых положений своими словами и т.п.

4. Прием использования стимулирующих звеньев.

Последовательность мыслей (А, В) легче запоминается, когда между ними присутствует мысль М, т.е. последовательность приобретает вид (А;М; В). При этом мысль М называют стимулирующим звеном. Например, при решении примера 23·4 ученик после записи 23·4=(20+3)·4 повторяет правило умножения суммы на число и продолжает 20·4+3·4=92. В этом случае последовательность мыслей такова: 23·4 → правило → 92. Названное правило является стимулирующим звеном. Другим вариантом применения стимулирующих звеньев служит методика обучения учащихся свертыванию процесса рассуждения (см. данную главу, § 7).

В качестве стимулирующих звеньев при изучении математики могут выступать: 1) вспоминание по ходу решения задач, упражнений математических определений и правил; 2) применение полученных знаний в практической ситуации; 3) использование графических и схематических изображений; 4) работа учащихся с моделями, индивидуальными наглядными пособиями; 5) применение различных форм мышления, особенно аналогии.

Учителю надо научить учащихся тому, в каком месте, в какой момент вводится то или иное стимулирующее звено.

5. Прием выделения смысловых опорных пунктов.

В ходе чтения текст мысленно делится на логические части, каждый из которых получает краткое заглавие в виде отдельных слов или выражений. Такие заглавия, образы, слова и т.п. в психологии называют смысловыми опорными пунктами. По существу они представляют из себя как бы план изучаемого материала. После соответствующего их оформления можно получить так называемые опорные конспекты. В математике начальных классов данный прием используется в виде опорных схем при решении задач (гл. 6 § 1).

Одним из вариантов данного приема является прием запоминания с помощью символов, применяемый в опыте многих учителей. Например, для запоминания приема вычитания числа из суммы на первых порах учащимся помогает оформление записей в такой форме:

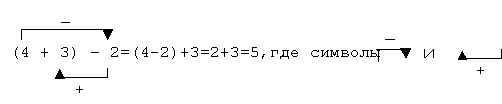
наглядно показывают порядок действий. Это особенно важно для средних и слабых учащихся.

Для развития математической памяти можно использовать специально подобранную систему задач. В частности, в начальных классах оправдывает себя применение следующих видов задач.

1. Задачи с лишними данными используются для обучения учащихся запоминанию отношений между числами - данными задачи. Учащиеся должны помнить, что означает "на ... больше", "в ... больше" и т.п. и как они связаны с данными задачи. Например, решая предложенную задачу с лишними данными (см. с.80), они должны помнить, что "на 3 грядки больше" обязательно должно быть связано с данными и проверить эту связь. Это даст им возможность обнаружить лишнее данное. Эта привычка воспитывается с трудом. Поэтому одну и ту же задачу полезно предлагать учащимся несколько раз с небольшими интервалами (через 2-3 урока) и проследить за их деятельностью. По мере того, как они научились уже до решения

отбросить лишнее данное, переходят к другим нижеперечисленным задачам.

2. Нереальные задачи развивают способности учащихся запоминать приблизительные значения числовых значений величин, встречающихся в жизненной ситуации (скорость пешехода, возраст животных и т.п.).

3. Задачи с несколькими решениями способствуют лучшему запоминанию конкретного смысла арифметических действий, связей между их компонентами, связей между величинами, способов решения задач и т.п. Например, решив задачу: "За 4 кг яблок уплатили 28 рублей. Сколько уплатили за 8 кг яблок?" двумя способами:

1 способ: 1) 28:4=7 (р.) - стоит 1 кг яблок.

2) 7·8=56 (р.) - стоит 8 кг яблок.

2 способ: 1) 8:4=2 (раза) - больше купили яблок.

2) 28·2=56 (р.) - стоит 8 кг яблок,

учащимся рекомендуем запоминать, что в одних случаях можно решить нахождением цены предмета, а в других - учитывая увеличение количества предметов в несколько раз.

С.И. Волкова и Н. Н. Столярова, в своей программе развития познавательных способностей учащихся, для развития памяти рекомендуют следующие виды упражнений (см.(19)-(25)). Заметим, что при их выполнении учитель заранее дает установку на запоминание и разъясняет ход дальнейших действий учащихся, в том числе и своей.

1. Математические слова. Учитель называет несколько слов: треугольник, отнять, восемь, столько же, пример, математика, четыре, получится и просит учащихся запомнить из них как можно больше. При проверке один ученик называет слова, другие добавляют. Анализируя количество названных слов, выясняют причины запоминания одних и не запоминания других.

2. Цепочка слов. Учитель называет по три слова, связанных по смыслу: круг, треугольник, квадрат; плюс, минус, равняется; шесть, четыре, два и т.д. Затем учитель снова называет первое слово, а второе и третье слова называют учащиеся по одному или хором. При анализе подчеркивается, что слова, связанные по смыслу, запоминаются легче.

3. Повтори-ка! Учитель называет слово (например, пять). Ученик повторяет это слово и добавляет другое (пять, квадрат). Следующий ученик перечислив ранее названные слова, добавляет свое (пять, квадрат, больше) и т.д. Тот, кто не сумеет повторить всех слов или перепутает их порядок - выбывает из игры. Побеждает тот, кто остается, т.е. у кого лучше память.

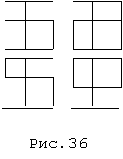
4. Зрительный диктант. В течение одной минуты учитель показывает фигуры (рис.36) и просит их запомнить. Учащиеся, в свою очередь, внимательно смотрят, прорисовывают в воздухе, стараясь запомнить очертанияфигуры, чтобы затем точнее нарисовать в тетради или на листе бумаги. После результаты проверяются.

В зависимости от класса все эти задания имеют разную степень трудности. Все они в основном предназначены для развития внимания, восприятия, зрительной и слуховой памяти.

Таким образом, развитие математической памяти должно быть целенаправленной работой. Учитель должен не только фиксировать умение запоминать а, прежде всего, должен обучать учащихся рациональной технологии запоминания и убедить их в том, что результаты будут не сразу, а постепенно.