3. Обучение восприятию и умению наблюдать.

Восприятие является одним из важных средств познания ребенком действительности. Его развитие должно быть целенаправленным и организованным процессом.

Исследованиями ученых-психологов установлено:

1) детей надо специально учить восприятию, чтобы они не сохранили типичные для их возраста неточность, нерасчлененность восприятия;

2) обучение должно быть направлено на совершенствование анализа и обобщения и при этом анализ должен вести к синтезу, к установлению связей, к обобщению;

3) чем моложе дети, тем большую роль в обучении восприятию играют их практические действия;

4) в обучении восприятию огромную роль играет включение речи.

Как известно, обучение детей восприятию обычно проходит через формирование культуры наблюдения. В данном процессе особенно важно умелое сочетание деятельности учителя и учащихся. Об одном из таких вариантов мы уже говорили (см.гл.2, § 1).

На уроках математики восприятие и наблюдательность формируются также и через специально подобранную систему заданий. Остановимся на них более конкретно.

1. Упражнения на развитие восприятия.

Рассматривая различные виды упражнений, С.И. Волкова и Н. Н. Столярова пишут: "...восприятие более чем какой-либо другой познавательный процесс связано с другими познавательными процессами, в частности, с воображением, памятью, мышлением, а потому большая часть заданий этой группы будет находиться в группах заданий, соответствующих названным познавательным процессам" (21, с. 55-56).

Основными видами заданий на развитие и совершенствование восприятия в начальном курсе математики являются задания на развитие восприятия формы: предлагается наложить на геометрические фигуры разной формы то тонкую веревочку, то счетные палочки, то мягкую проволоку для того, чтобы воспринять разницу в их формах (круглые, некруглые); обвести контуры различных геометрических фигур различными цветными карандашами; изготовить из листа бумаги путем его перегибания модели различных геометрических фигур; определить взаимное расположение фигур на плоскости и в пространстве; начертить и зарисовать различные геометрические фигуры, в том числе фигуры сложной конфигурации с использованием точечной основы; увеличить (уменьшить) заданную фигуру (рисунок) в заданном масштабе.

Используются также задания на развитие глазомера: сравнить "на глаз" линейные величины (длины), плоскостные (площади), пространственные (объемы) и провести проверку получаемого результата сначала путем практического наложения измеряемых фигур, затем с помощью измерительных инструментов, а в последующем и путем проведения соответствующих вычислений. Ниже приводим некоторые из названных видов упражнений.

1) Упражнения на восприятие формы.

а) Попробуй наложить на каждую фигуру: а) тонкую веревочку, б) счетные палочки (спички), в) мягкую проволоку (рис. 17).

б) Проведи синие стрелки от черных треугольников к белому и зеленые стрелки – от черных квадратов белому (рис. 18).

в) Используя линейку-трафарет, нарисуй справа столько же квадратов, сколько нарисовано кругов (рис.19).

г) Нарисуй справа по точкам такую же букву "Т", как и слева. Раскрась ее коричневым карандашом (рис. 20).

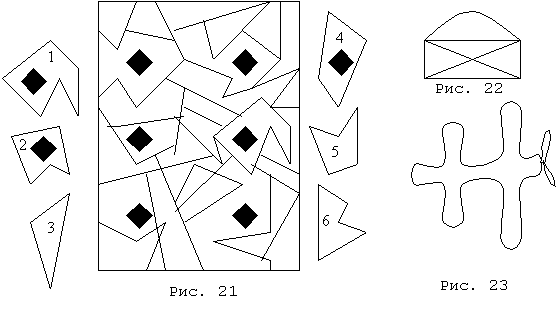
д) Напиши номер плитки, выпавшей из мозаики (рис.21).

е) Не отрывая карандаша от бумаги и не проводя одну и ту же линию дважды, попробуй нарисовать эту фигуру (рис. 22, 23).

2) Упражнения на развитие глазомера.

а) Найди «на глаз» отрезок, длина которого точно равна высоте нарисованного домика. Проверь себя, измерив высоту домика и длины заданных отрезков (рис. 24)

б) Определи на глаз длину отрезков в сантиметрах и проверь измерением (рис. 25).

в) Построй 3 квадрата сначала из 17 счетных палочек, а затем из 18. В результате дети должны получить фигуры, изображенные на рис. 26.

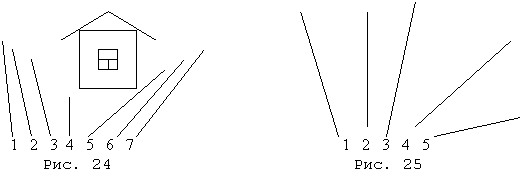
Рис. 26

г) Из пункта А велосипедист проехал 10 км на восток, затем повернул на север и проехал еще 20 км, после чего ехал на запад 10 км и на юг - 10 км. Наконец, опять повернул на восток и проехал 10 км. Напишите как можно больше ответов, на что похоже изображение пути велосипедиста.

При решении данного задания, дети мысленно прослеживают путь велосипедиста, затем вычерчивают его на бумаге.

2. Задачи на развитие восприятия.

Исследуя математические способности школьников, В.А. Крутецкий использовал систему экспериментальных задач (48, с. 118-123). Многие из этих задач могут быть с успехом использованы учителем для развития способностей учащихся, в том числе и восприятия.

1) Задачи с несформулированным вопросом.

 З а д а ч а: Надя решила 10 примеров, а Вера 12 примеров. (На сколько примеров больше решила Вера?)

Такие задачи предлагаются без вопроса и учитель просит быстрее "решить". Обязательно находятся учащиеся. которые тут же записывают решение в виде 10+12=22 (примера), не задумываясь о наличии вопроса (если до сих пор они в основном решали задачи на нахождение суммы).

Учитель должен дать возможность "ошибиться", а потом уже их "пожурить"и анализируя текст вместе подобрать вопрос, логически вытекающий из данных задачи.

2) Задачи с недостающими данными.

З а д а ч а: На обивку кресел требуется 40 м ткани. Израсходовали 32 м ткани. Сколько кресел обили? (Неизвестно число кресел, на которые израсходовали 40 м ткани).

В таких задачах отсутствие некоторых данных лишает возможности дать точный ответ на поставленный вопрос. Подобрать нужное данное можно только после полного восприятия конкретных данных задачи и отношений между ними. Надо учить учащихся воспринимать формальную структуру задачи. Очень часто недостаток данных проявляется после краткой записи задачи.

3) Задачи с лишними данными

З а д а ч а: Школьники пропололи 8 грядок моркови и 11 грядок свеклы, что на 3 грядки больше, чем моркови. Сколько грядок всего пропололи школьники? (Лишнее данное: на 3 грядки больше.)

В таких задачах некоторые данные (на 3 грядки больше) логически вытекают из других данных (8 грядок и 11 грядок) и не влияют на решение задачи. Отсутствие привычки предварительного восприятия структуры задачи, отношений между данными приводит к тому, что при решении некоторые учащиеся, а порою большинство, использует и это лишнее данное.

Данную задачу часто решают так: 8+11+3=22 (гр.). У учащихся утвердилось ложное мнение: если в условии есть число, то оно в решении обязательно должно быть использовано. Опыт показывает, что по мере увеличения числа таких задач на уроках многие учащиеся, без предварительного анализа условия, к решению не приступают.

4) Задачи с взаимопроникающими элементами.

З а д а ч а: Сколько треугольников на чертеже (рис.13)?

Такие задачи, в основном, предлагаются на геометрическом материале, где отдельные элементы фигур взаимопроникают", т.е. часть одной фигуры или же фигура целиком входит в другую фигуру.

Предлагая эти задачи, учитель обучает учащихся восприятию геометрических фигур через анализ, т.е. разбиением на части.

5) Нереальные задачи.

З а д а ч а: Пешеход шел со скоростью 28 км/ч. Какое расстояние он прошел за 3 часа?

Как правило, учащиеся эту задачу решают "без ошибок" и записывают ответ: 84. Они не приучены в ходе восприятия условия задачи данные числа сопоставлять с реальной ситуацией. В реальной жизни скорость пешехода не превышает 10 км/ч. Отсутствие жизненного опыта мешает им заметить нереальность некоторых данных задачи. Предлагая их вниманию такие задачи, учитель, наряду с обучением математике, формирует у них и определенный жизненный опыт.

В системе развивающего обучения эти задачи имеют большую ценность. В частности, задачи вида 1-4 нашли достойное место в системе обучения Л.В. Занкова.

Изучив вопросы развития восприятия, психолог И.В. Дубровина делает следующие выводы: "Малоспособные к математике учащиеся обычно воспринимают разрозненные данные задачи. Они с трудом справляются со специальной работой по "связыванию" этих данных в систему. Помощь экспериментатора, объяснения, тренировочные упражнения являются действенными лишь тогда, когда они носят настойчивый и продолжительный характер. Не воспринимая комплекса отношений, эти учащиеся обычно не могут опре-

делить, каких данных в задаче недостает или какие являются излишними. Они упорно пытаются решить задачу с недостающими данными или использовать все данные, не пытаясь даже дать себе отчет, нужны ли они для решения задачи.

У учащихся групп очень способных и способных, довольно четко проявляется установка воспринимать в условии задачи не просто отдельные величины, а именно отношения представленных в задаче величин. Это дает им возможность легко вычленить именно те данные, которые необходимы и достаточны для решения задачи, ясно осознавать, каких величин недостает для этого, какие являются лишними, ненужными. Отчетливо представляя себе соотношения величин, способные дети не испытывают затруднений при постановке несформулированного вопроса" (30, с. 19-20).